A staircase has 5 steps each 10 cm high and 10 cm wide. What is the minimum horizontal velocity to be given to the ball so that it hits directly the lowest plane from the top of the staircase? (g=10ms−2)
2ms−1
1ms−1
√2ms−1
12ms−1
The correct Answer is:B
To solve the problem of finding the minimum horizontal velocity required for a ball to hit the lowest plane from the top of a staircase with 5 steps, each 10 cm high and 10 cm wide, we can follow these steps:
Step 1: Determine the Total Height
The total height of the staircase can be calculated by multiplying the height of each step by the number of steps.
Total Height=Height of each step×Number of steps=10cm×5=50cm
Convert this height into meters:
Total Height=50cm=0.50m
Step 2: Calculate the Time of Flight
Using the equation of motion for vertical displacement, we can find the time it takes for the ball to fall this height. The formula is:
h=12gt2
Where:
- h=0.50m
- g=10m/s2
Rearranging the formula to solve for t:
0.50=12×10×t2
0.50=5t2
t2=0.505=0.10
t=√0.10=0.316s
Step 3: Determine the Horizontal Distance
The horizontal distance that the ball needs to travel is equal to the total width of the staircase, which can also be calculated:
Total Width=Width of each step×Number of steps=10cm×5=50cm=0.50m
Step 4: Calculate the Minimum Horizontal Velocity
Using the formula for horizontal motion, where horizontal distance d is given by:
d=u⋅t
Where:
- d=0.50m
- t=0.316s
Rearranging to solve for u:
u=dt=0.500.316≈1.58m/s
Conclusion
The minimum horizontal velocity u required for the ball to hit the lowest plane from the top of the staircase is approximately:
1.58m/s
The total height of the staircase can be calculated by multiplying the height of each step by the number of steps.
Using the equation of motion for vertical displacement, we can find the time it takes for the ball to fall this height. The formula is:
- h=0.50m
- g=10m/s2
The horizontal distance that the ball needs to travel is equal to the total width of the staircase, which can also be calculated:
Using the formula for horizontal motion, where horizontal distance d is given by:
- d=0.50m
- t=0.316s
The minimum horizontal velocity u required for the ball to hit the lowest plane from the top of the staircase is approximately:
Topper's Solved these Questions
Similar Questions
The thermal capacity of a substance is 5 cal/∘F. What is water equivalent of the substance
View SolutionWhich type of cell be used if a device requires 75A of current for 15 seconds?
View SolutionA staircase contains three steps each 10 cm high and 20 cm wide figure. What should be the minimum horizontal velocity of a bal rolling off the upper most plane so as to hit directly the lowest plane?
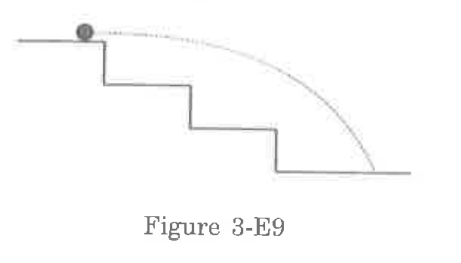
View SolutionA staircase contains four steps each 20cm high and 40cm wide. What should be the minimum horizontal velocity of a ball rolling off the uppermost plane so as to hit directly the lowest plane ?
View SolutionA staircase contains four steps each 10cm high and 20cm wide. The minimum horizontal velocity of a ball rolling off the uppermost plane so as to hit directly the lowest plane is
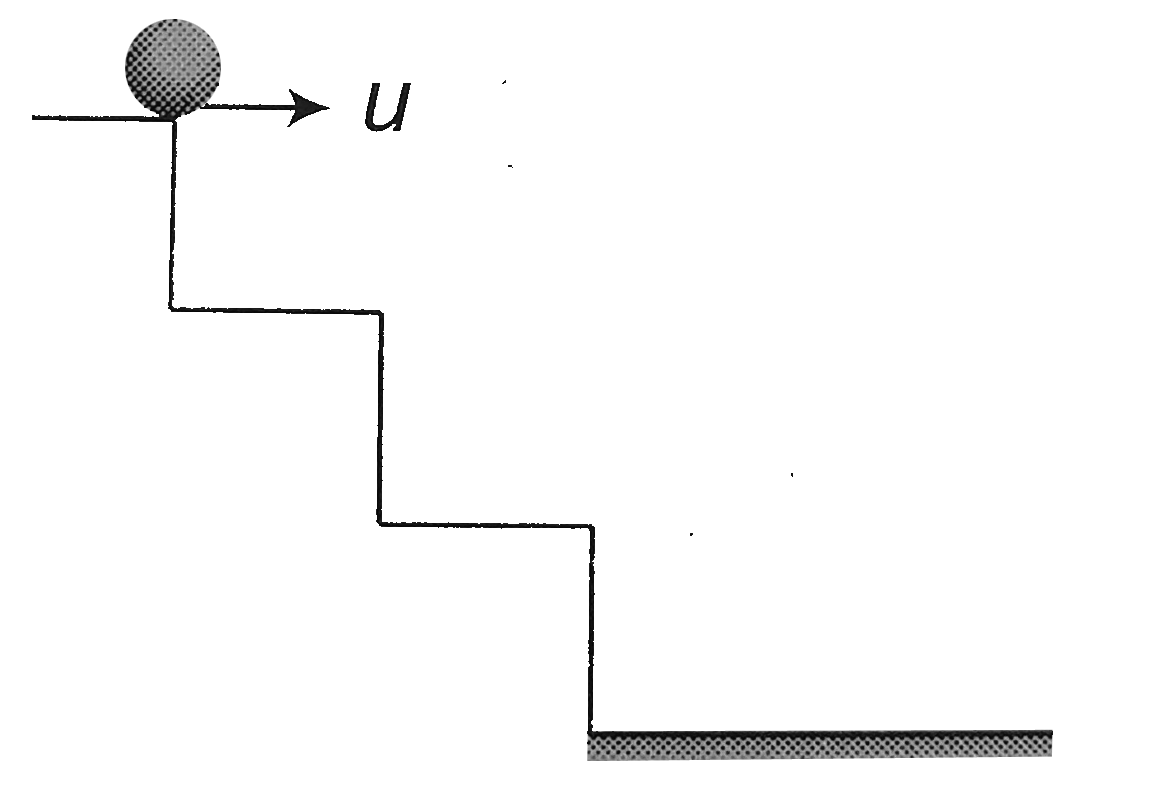
View Solution[" A staircase has steps each of "],[" height "20cm" and width "40cm" .A "],[" ball rolls off the top of the "],[" staircase horizontally with "],[" velocity "5m/s" .The ball hits the "],[" nth step from the top at the first "],[" bounce,then "n=..........." (take "],[g=10ms-2)]
View SolutionA staircase contains three steps each 10 cm high and 20 cm wide as shown in the figure. What should be the minimum horizontal velocity of a ball rolling off the uppermost plane so as to hit directly the edge of the lowest plane ? [g=10m/s2]
View SolutionThe height and width of each step of a staircase are 20cm and 30cm respectively. A ball rolls off the top of a stair with horizontal velocity v and hits the fifth step. The magnitude of v is (g=10 ms−2)
View SolutionA sphere rolls off the top of a stairway with a horizontal velocity of magnitude 200 cm/sec. The steps are 10 cm high and 10 cm wide. Which step will the ball hit first?(g=10 m/s2)
View SolutionA staircase contains three steps each 10 cm high and 20 cm wide as shown in the figure. What should be the minimum horizontal velocity of a ball rolling off the uppermost plane so as to hit directly the edge of the lowest plane ? [g=10m/s2]
View SolutionThe height and width of each step of a staircase are 20cm and 30cm respectively. A ball rolls off the top of a stair with horizontal velocity v and hits the fifth step. The magnitude of v is (g=10 ms^(-2))
View SolutionA staircase contains three steps each 10 cm high and 20 cm wide figure. What should be the minimum horizontal velocity of a bal rolling off the upper most plane so as to hit directly the lowest plane?

View SolutionA staircase contains three steps each 10 cm high and 20 cm wide as shown in the figure. What should be the minimum horizontal velocity of a ball rolling off the uppermost plane so as to hit directly the edge of the lowest plane ? [g=10m/s2]
View SolutionThe height and width of each step of a staircase are 20 cm and 30 cm respectively. A ball rolls off the top of a stair with horizontal velocity v and hits the fifth step. The magnitude of v is (g = 10 ms^(-2))
View SolutionA sphere rolls off the top of a stairway with a horizontal velocity of magnitude 200 cm/sec. The steps are 10 cm high and 10 cm wide. Which step will the ball hit first ? (g=10m/s2)
View Solution