For a simple pendulum, the graph between T2andL (where T is the time period & Lis the length) is
straight line passing through origin
parabolic
circle
none of the above
The correct Answer is:A
straight line passing through origin
Topper's Solved these Questions
Similar Questions
The time period of a simple pendulum is given by the formula, T=2π√l/g, where T = time period, l = length of pendulum and g = acceleration due to gravity.
If the length of the pendulum is decreased to 1/4 of its initial value, then what happens to its frequency of oscillations ?
View SolutionThe time period of a simple pendulum is given by the formula, T=2π√l/g, where T = time period, l = length of pendulum and g = acceleration due to gravity.
If the length of the pendulum is decreased to 1/4 of its initial value, then what happens to its frequency of oscillations ?
View Solution
Knowledge Check
For a simple pendulum the graph between length and time period will be
AhyperbolaBparabolaCstraight lineDnone of theseThe l−T2 graph of a simple pendulum is an shown in the figure. The time period of the pendulum of length 0.5 mm is
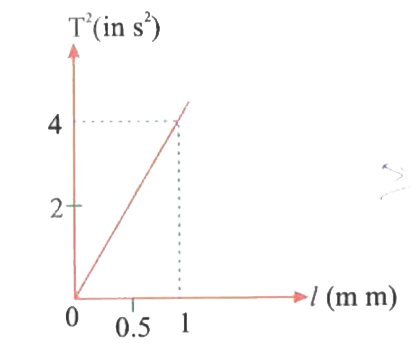 A1sB1.2 sC√2 sD1√2s
A1sB1.2 sC√2 sD1√2sTime period of a simple pendulum of length L is T1 and time period of a uniform rod of the same length L pivoted about one end and oscillating in vertical plane is T2. Amplitude of oscillation in both the cased is small. The T1/T2 is:
A√2/√3B1/√3C√3/√2D1/√2
A simple pendulum of length 'l' and time period 'T' on earth is taken onto the surface of moon. How should the length of the simple pendulum be changed on the moon such that the time period is constant.
(Take ge=6gm)
View SolutionThe graph between the length and square of the period of a simple pendulum is a
View SolutionTime period of a simple pendulum of length L is T1 and time period of a uniform rod of the same length L pivoted about an end and oscillating in a vertical plane is T2. Amplitude of osciallations in both the cases is small. Then T1T2 is
View SolutionA simple pendulum of length l1 has a time period of 4 s and another simple pendulum of length l2 has a time period 3 s. Then the time period of another pendulum of length (l1−l2) is
View SolutionThe time period of a simple pendulum in a stationary train is T. The time period of a mass attached to a spring is also T. The train accelerates at the rate 5 ms−2. If the new time periods of the pendulum and spring be TpandTs, respectively. Then,
View Solution
