The displacement-time graph of a particle acted upon by a constant force is
a straight line
a circle
a parabola
any curve depending upon initial conditions
The correct Answer is:C
To solve the question regarding the displacement-time graph of a particle acted upon by a constant force, we can follow these steps:
Step 1: Understand the relationship between force, mass, and acceleration
According to Newton's second law of motion, the force acting on an object is equal to the mass of the object multiplied by its acceleration. This can be expressed as:
F=ma
Step 2: Relate acceleration to displacement and time
When a constant force acts on a particle, it causes a constant acceleration. The equations of motion describe the relationship between displacement (s), initial velocity (u), time (t), and acceleration (a). One of the key equations is:
s=ut+12at2
Step 3: Analyze the equation for displacement
In the equation s=ut+12at2, we can see that:
- The term ut represents the linear displacement due to the initial velocity.
- The term 12at2 represents the additional displacement due to constant acceleration.
Step 4: Identify the shape of the graph
The equation s=ut+12at2 is a quadratic equation in terms of time t. When plotted on a graph with displacement (s) on the y-axis and time (t) on the x-axis, this equation will produce a parabolic curve.
Step 5: Conclusion
Since the displacement-time graph of a particle acted upon by a constant force is a quadratic function of time, we conclude that the graph is a parabola. Therefore, the correct answer is:
Option C: Parabola.
---
According to Newton's second law of motion, the force acting on an object is equal to the mass of the object multiplied by its acceleration. This can be expressed as:
F=ma
When a constant force acts on a particle, it causes a constant acceleration. The equations of motion describe the relationship between displacement (s), initial velocity (u), time (t), and acceleration (a). One of the key equations is:
s=ut+12at2
In the equation s=ut+12at2, we can see that:
- The term ut represents the linear displacement due to the initial velocity.
- The term 12at2 represents the additional displacement due to constant acceleration.
The equation s=ut+12at2 is a quadratic equation in terms of time t. When plotted on a graph with displacement (s) on the y-axis and time (t) on the x-axis, this equation will produce a parabolic curve.
Since the displacement-time graph of a particle acted upon by a constant force is a quadratic function of time, we conclude that the graph is a parabola. Therefore, the correct answer is:
Option C: Parabola.
Topper's Solved these Questions
Similar Questions
Knowledge Check
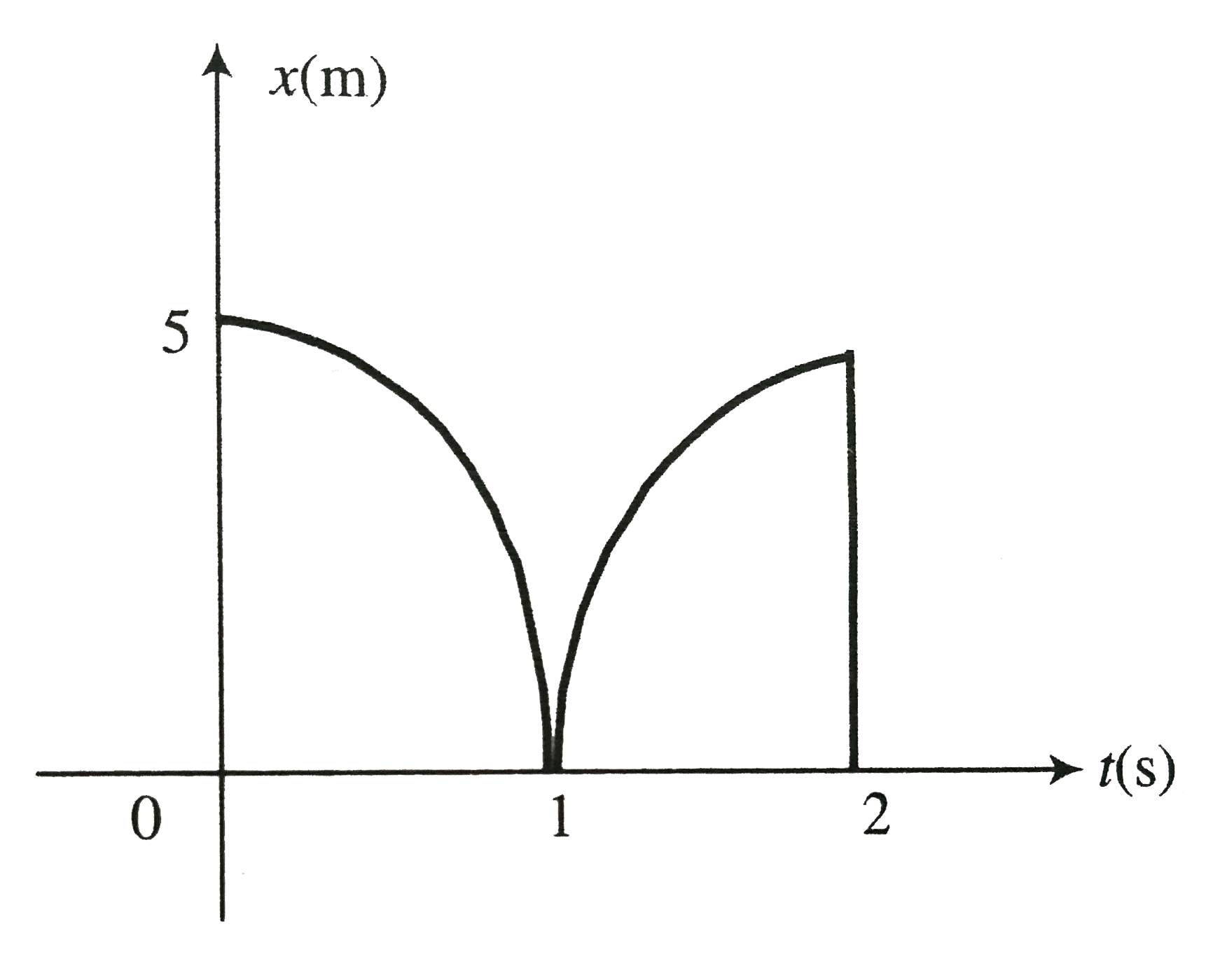
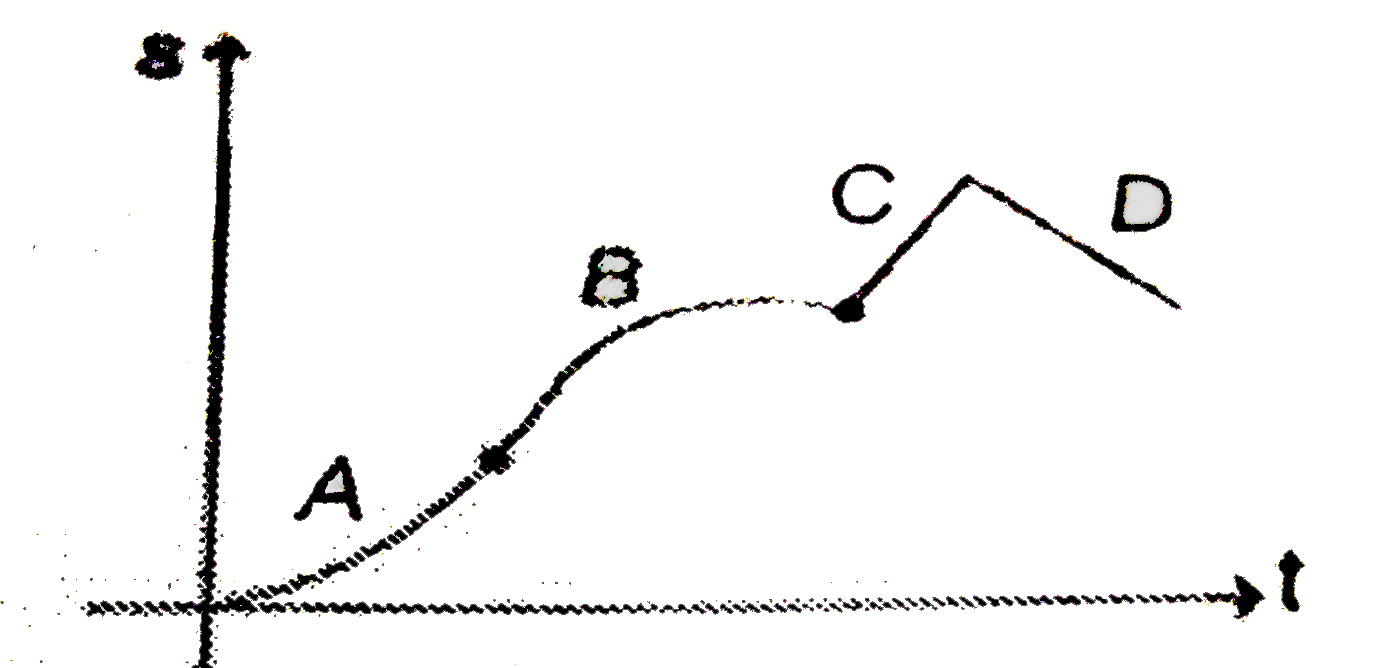
The displacement-time graph of a moving particle with constant acceleration is shown in. The velocity-time is given by
 .A
.A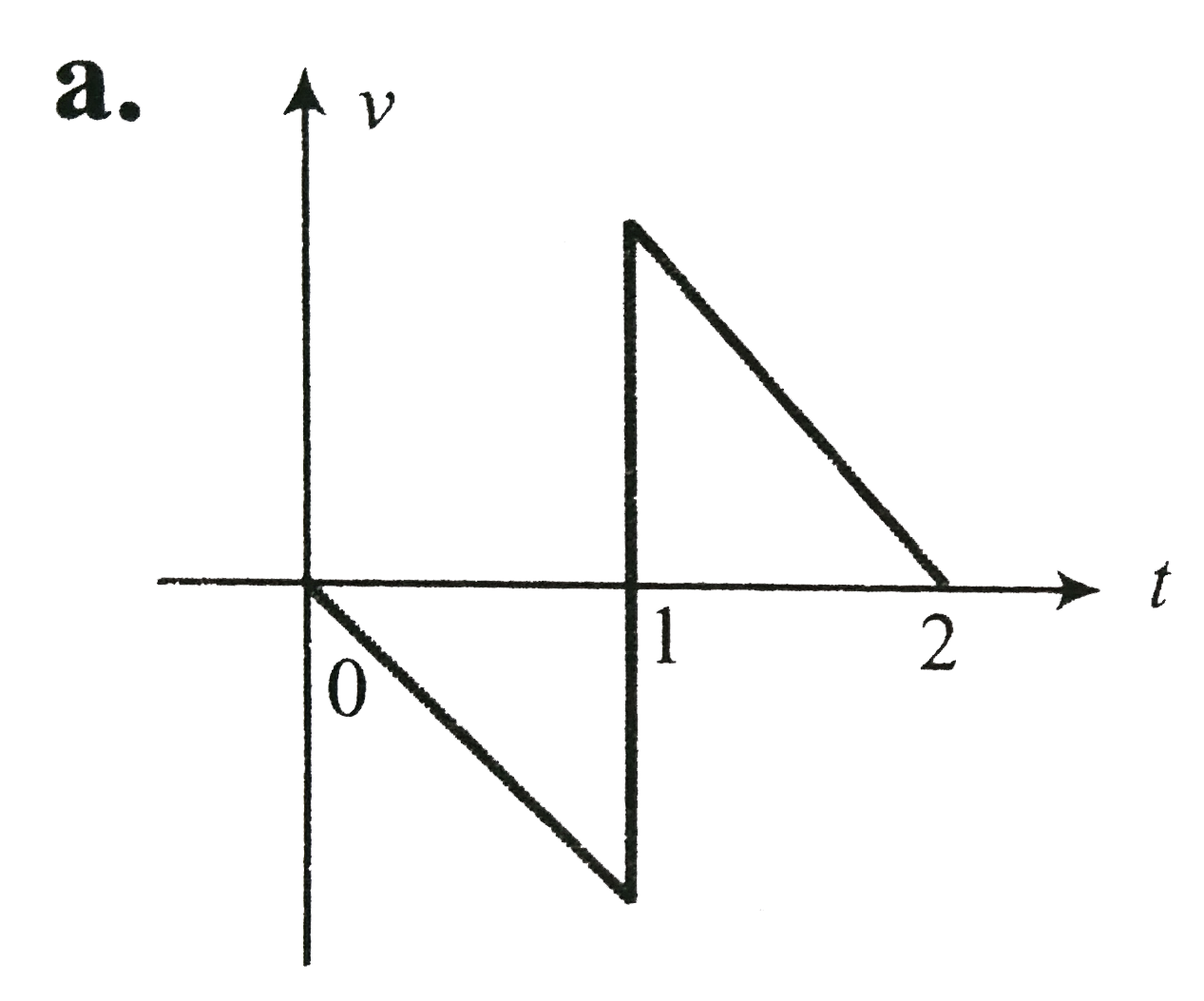 .B
.B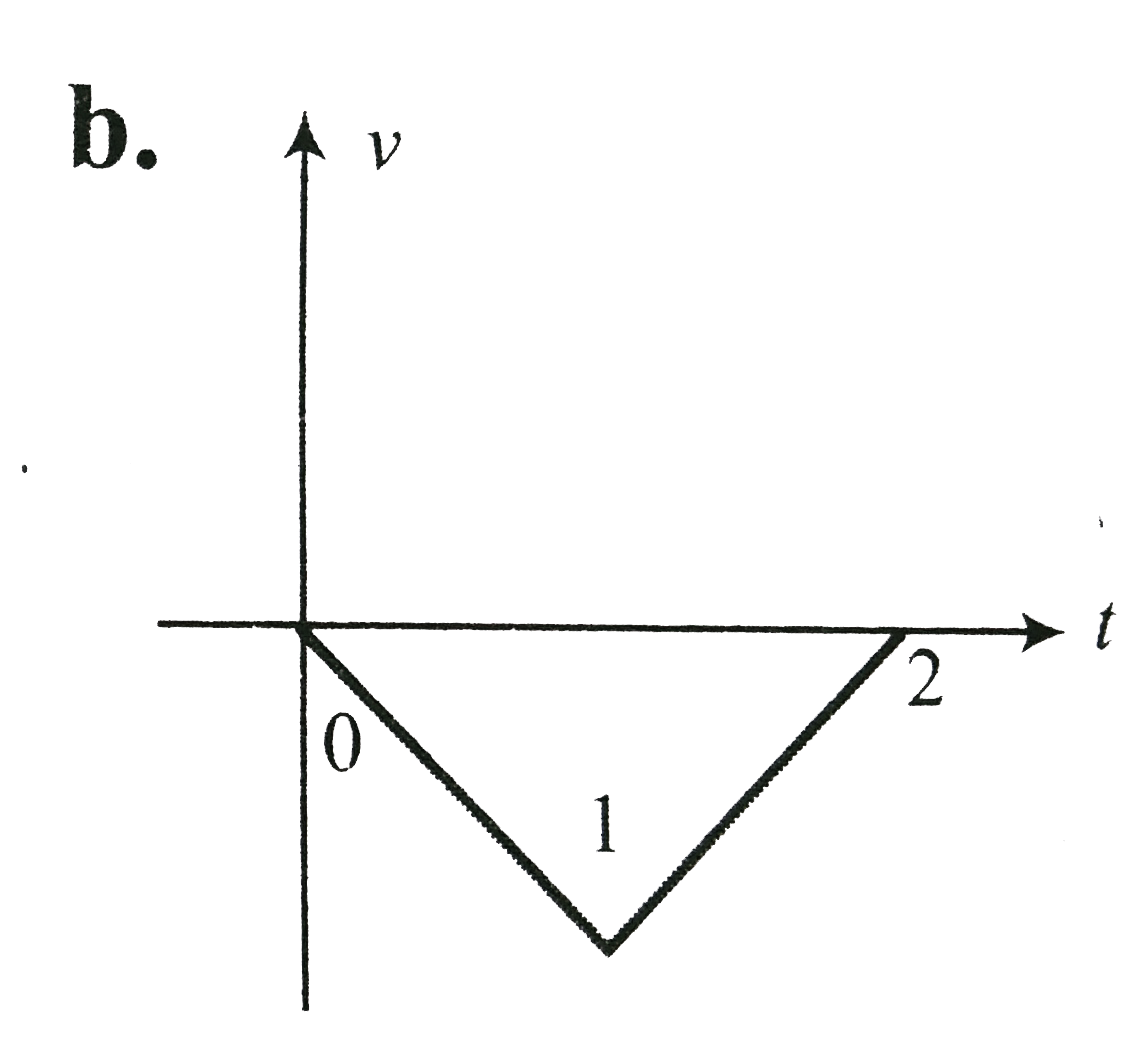 .C
.C .D
.D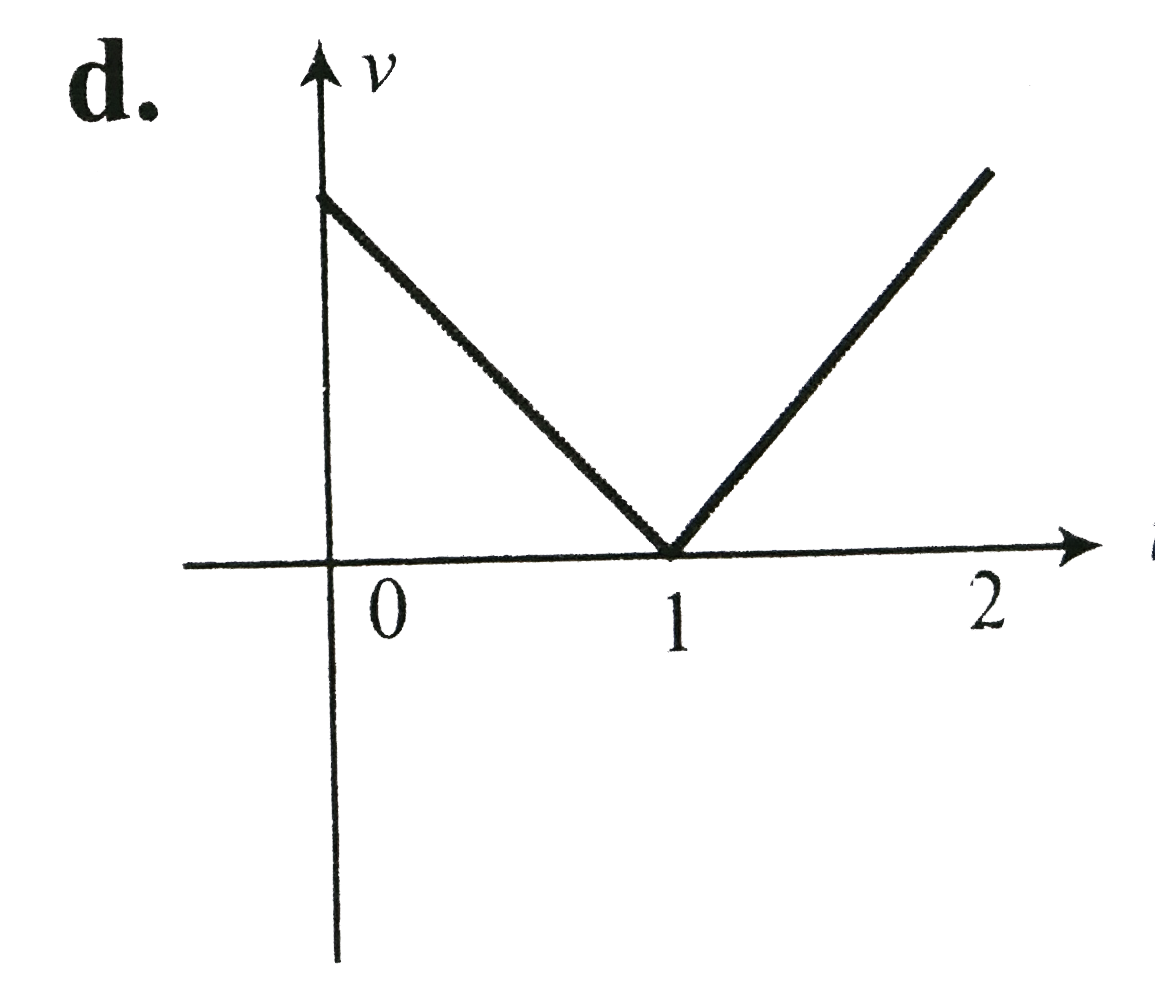 .
.Figure show the displacement - time graph of a particle moving on the x-axis
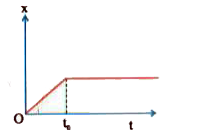 Athe particle is continuously going in positive X directionBthe particle is at restCthe velocity increases up to a time t0 and then becomes constant.Dthe particle moves at constant velocity up to a time t0 and then stops.
Athe particle is continuously going in positive X directionBthe particle is at restCthe velocity increases up to a time t0 and then becomes constant.Dthe particle moves at constant velocity up to a time t0 and then stops.The displacement-time graph of a particle is as shown below. It indicates that
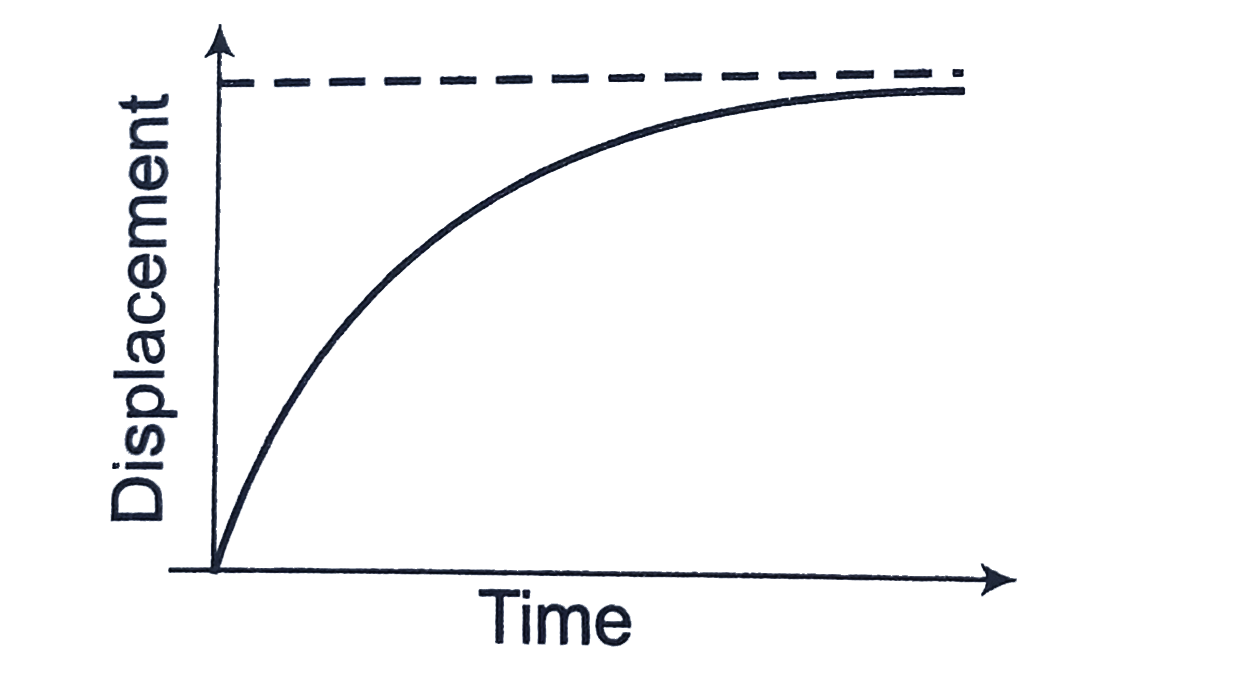 Athe particle starts with a certain velocity but the motion is retarded and finally the particle stopsBthe velocity of the particle is constant throufgoutCthe acceleration of the particle is constant throughoutDthe particle starts with a velocity, the motion is accelerated and finally the particle moves with a constant velocity
Athe particle starts with a certain velocity but the motion is retarded and finally the particle stopsBthe velocity of the particle is constant throufgoutCthe acceleration of the particle is constant throughoutDthe particle starts with a velocity, the motion is accelerated and finally the particle moves with a constant velocity
The displacment-time graph of a particle moving with respect to a reference point is a straight line
View SolutionThe displacement time graph of a particle executing S.H.M. is as shown in the figure
The corresponding force-time graph of the particle is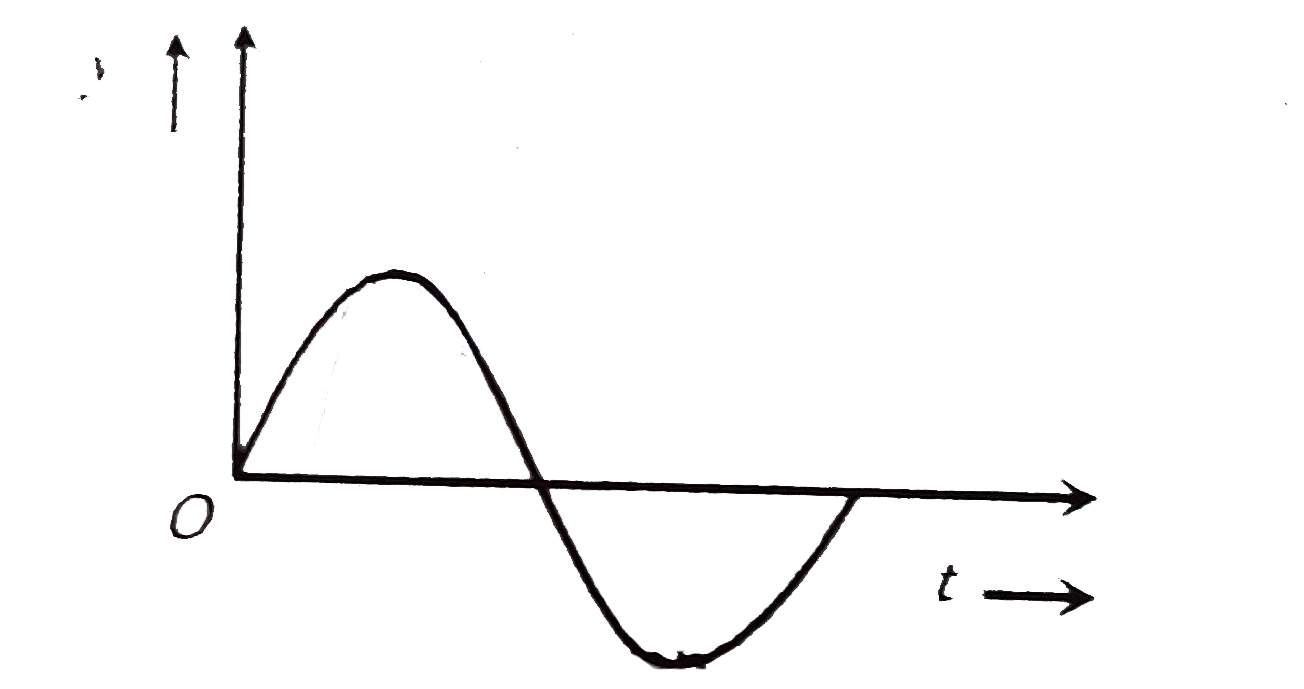
View SolutionDescribe the motion of a particle acted upon by the force:
View SolutionDisplacement-time graph of a particle executing SHM is as shown

The corresponding force-time graph of the particle can be
View SolutionDisplacement time graph of a particle moving in a straight line is a shown in figure.
View Solution