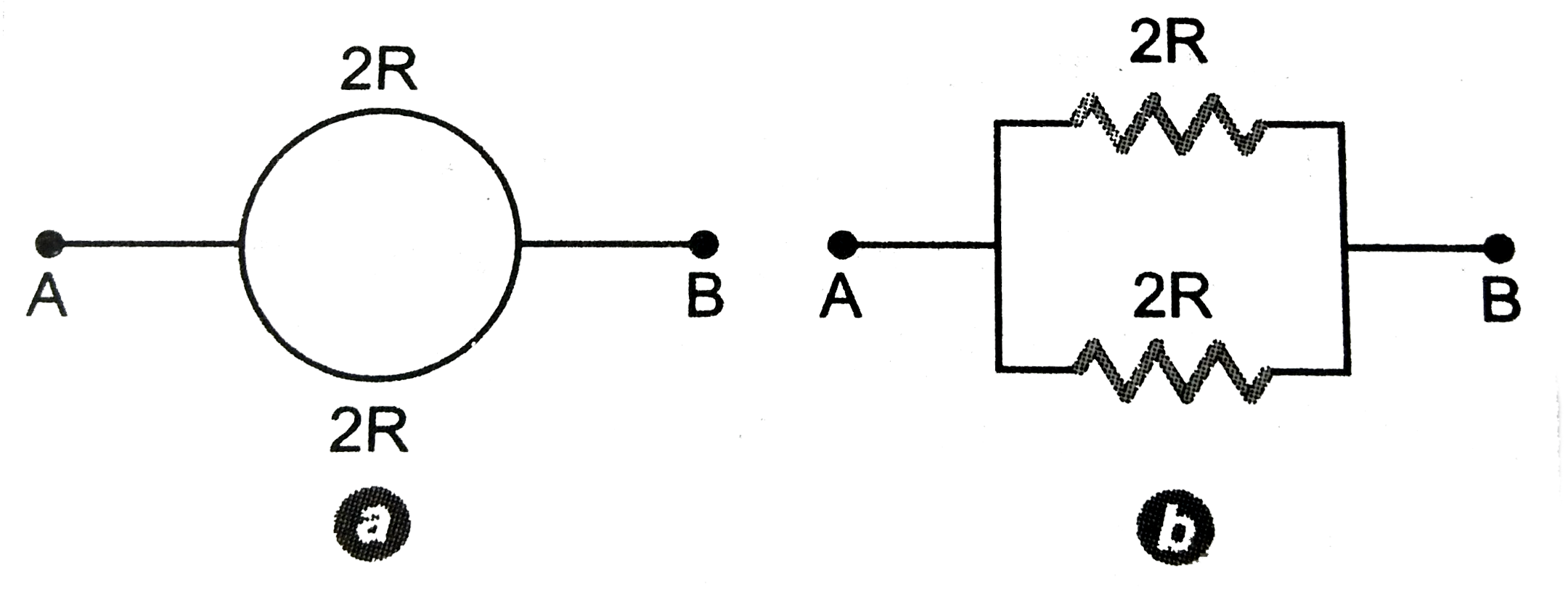
The effective resistance of two wires is 2 x. The resistance of one wire is two times of the other wire and is three times the effective resistance. Which one of the following is correct in respet of value of x ?
x can take only one value.
x must only be greater than or equal to 1
x can take any positive real value
The information given above is inconsistent
The correct Answer is:C
To solve the problem step by step, let's define the resistances and analyze the information given.
Step 1: Define the resistances
Let the resistance of the first wire be R1 and the resistance of the second wire be R2. According to the problem, we have:
- R1=2R2 (one wire is two times the other)
- The effective resistance Reff=2x
Step 2: Relate the resistances to the effective resistance
It is given that R1 is three times the effective resistance:
R1=3×Reff=3×2x=6x
Step 3: Substitute R1 in terms of R2
From the relationship R1=2R2, we can substitute R1:
2R2=6x
Now, we can express R2 in terms of x:
R2=6x2=3x
Step 4: Calculate the effective resistance for parallel resistors
Since the effective resistance Reff is given as 2x and the resistors are in parallel, we can use the formula for parallel resistances:
1Reff=1R1+1R2
Substituting the values:
12x=16x+13x
Step 5: Simplify the equation
Finding a common denominator for the right side:
12x=16x+26x=36x=12x
This confirms our effective resistance calculation is consistent.
Step 6: Conclusion about x
Since there are no contradictions in our calculations, we conclude that x can take any positive real value.
Final Answer
Thus, the value of x can be any positive real number.
---
Let the resistance of the first wire be R1 and the resistance of the second wire be R2. According to the problem, we have:
- R1=2R2 (one wire is two times the other)
- The effective resistance Reff=2x
It is given that R1 is three times the effective resistance:
R1=3×Reff=3×2x=6x
From the relationship R1=2R2, we can substitute R1:
2R2=6x
Now, we can express R2 in terms of x:
R2=6x2=3x
Since the effective resistance Reff is given as 2x and the resistors are in parallel, we can use the formula for parallel resistances:
1Reff=1R1+1R2
Substituting the values:
12x=16x+13x
Finding a common denominator for the right side:
12x=16x+26x=36x=12x
This confirms our effective resistance calculation is consistent.
Since there are no contradictions in our calculations, we conclude that x can take any positive real value.
Thus, the value of x can be any positive real number.
Topper's Solved these Questions
Similar Questions
Knowledge Check
The resistance of a wire is 20ohm. It is so stretched that the length becomes three times, then the new resistance of the wire will be
A6.67 ohmsB60.0 ohmsC120 ohmsD180.0 ohmsThe resistance of a wire is 20ohm. It is so stretched that the length becomes three times, then the new resistance of the wire will be
A6.67 ohmB60 ohmC120 ohmD180 ohmThe resistance of wire is 20Ω. The wire is stretched to three times its length. Then the resistance will now be
A6.67ΩB60ΩC120ΩD180Ω
A wire of resistance 8R is bent in the form of a circle. What is the effective resistance between the ends of a diameter AB?
View SolutionA wire of resistance 8R is bent in the form of a circle. What is the effective resistance between the ends of a diameter AB ?
View SolutionThe resistance of a wire is 2Ω. The wire is stretched to doubel its length. Now the resistance of the wire will become
View SolutionA wire has a resistance of 12 ohm . It is bent in the form of equilateral triangle. The effective resistance between any two corners of the triangle is
View SolutionA wire has resistance of 24Ω is bent in the following shape. The effective resistance between A and B is
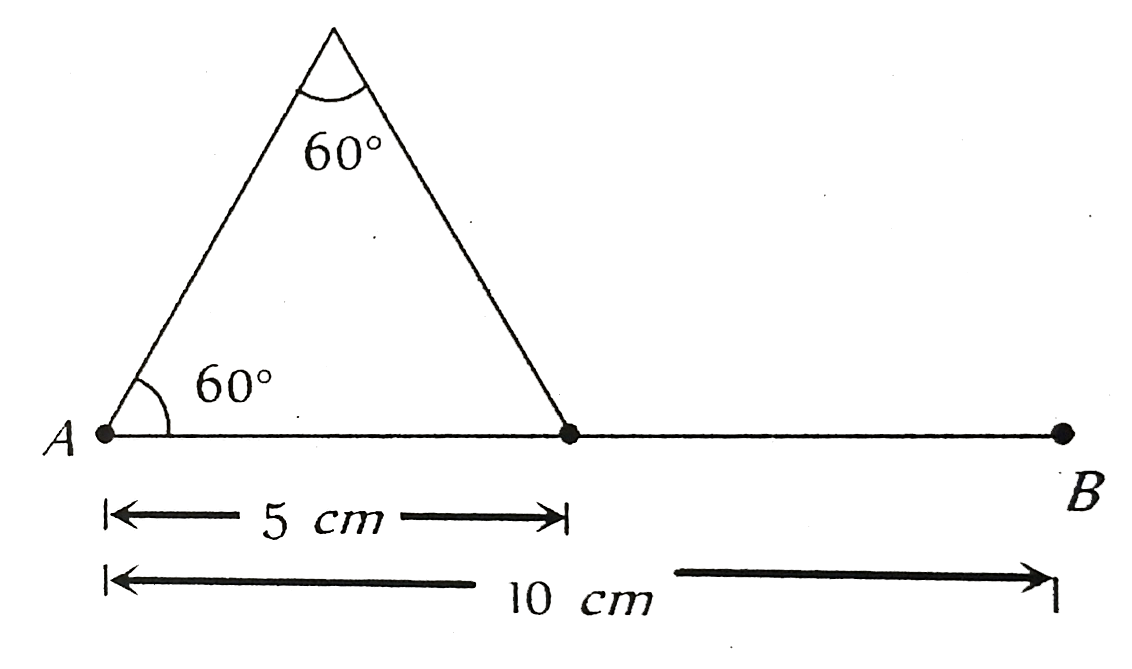
View Solution