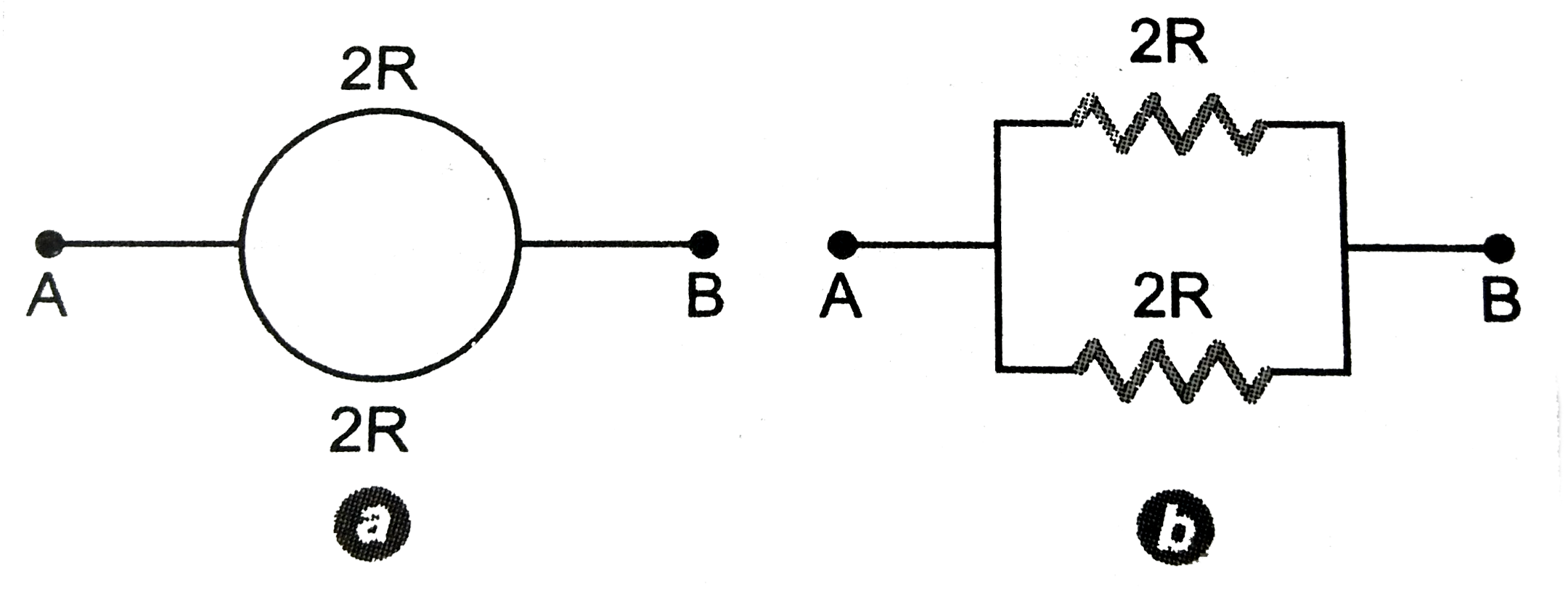
A wire of resistance 8R is bent in the form of a circle. What is the effective resistance between the ends of a diameter AB?

Video Solution

Text Solution

Generated By DoubtnutGPT

To find the effective resistance between the ends of a diameter AB of a wire bent in the form of a circle with a total resistance of 8R, we can follow these steps:
1. Understand the Configuration:
- The wire is bent into a circle, and we need to find the resistance between two points (A and B) that are at the ends of a diameter.
2. Divide the Circle:
- When the wire is bent into a circle, the total resistance of the wire is 8R. The wire can be thought of as being divided into two equal halves when considering the diameter AB.
- Each half of the wire will have a resistance of $\frac{8 R}{2} = 4 R$ .
3. Identify the Resistance in Parallel:
- The two halves of the wire (from A to the midpoint and from B to the midpoint) are in parallel when considering the effective resistance between A and B.
- Therefore, we have two resistances of 4R each in parallel.
4. Calculate the Equivalent Resistance:
- The formula for the equivalent resistance $R_{e q}$ of two resistors $R_{1}$ and $R_{2}$ in parallel is given by:
$\frac{1}{R_{e q}} = \frac{1}{R_{1}} + \frac{1}{R_{2}}$
- Here, $R_{1} = 4 R$ and $R_{2} = 4 R$ :
$\frac{1}{R_{e q}} = \frac{1}{4 R} + \frac{1}{4 R} = \frac{2}{4 R} = \frac{1}{2 R}$
- Therefore, the equivalent resistance $R_{e q}$ is:
$R_{e q} = 2 R$
5. Final Answer:
- The effective resistance between the ends of the diameter AB is $2 R$ .

Updated on:7/8/2024