If a charged particle (+q) is projected with certain velocity parallel to the magnetic field, then it will
trace helical path
trace circular path
continue its motion without any change
come to rest instantly
The correct Answer is:C
To solve the question, we need to analyze the behavior of a charged particle when it is projected parallel to a magnetic field.
1. Understanding the Force on a Charged Particle:
The force F acting on a charged particle moving in a magnetic field is given by the equation:
F=q⋅v⋅B⋅sin(θ)
where:
- q = charge of the particle,
- v = velocity of the particle,
- B = magnetic field strength,
- θ = angle between the velocity vector and the magnetic field vector.
2. Identifying the Angle:
In the case where the charged particle is projected parallel to the magnetic field, the angle θ is 0∘.
3. Calculating the Sine of the Angle:
The sine of 0∘ is:
sin(0∘)=0
4. Substituting into the Force Equation:
Substituting sin(0∘) into the force equation gives:
F=q⋅v⋅B⋅0=0
5. Conclusion on the Motion of the Particle:
Since the magnetic force F is zero, there is no force acting on the charged particle. Therefore, the particle will continue its motion without any change in velocity or direction.
Final Answer:
The charged particle (+q) will continue its motion without any change.
---
The force F acting on a charged particle moving in a magnetic field is given by the equation:
F=q⋅v⋅B⋅sin(θ)
where:
- q = charge of the particle,
- v = velocity of the particle,
- B = magnetic field strength,
- θ = angle between the velocity vector and the magnetic field vector.
In the case where the charged particle is projected parallel to the magnetic field, the angle θ is 0∘.
The sine of 0∘ is:
sin(0∘)=0
Substituting sin(0∘) into the force equation gives:
F=q⋅v⋅B⋅0=0
Since the magnetic force F is zero, there is no force acting on the charged particle. Therefore, the particle will continue its motion without any change in velocity or direction.
The charged particle (+q) will continue its motion without any change.
Topper's Solved these Questions
Similar Questions
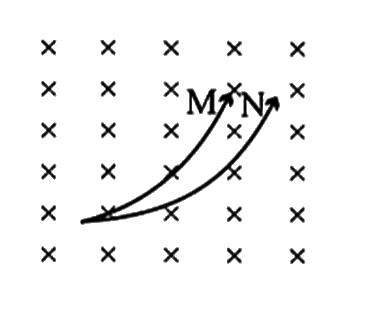
Two charged particle M and N are projected with same velocity in a uniform magnetic field. Then M and N respectively.
View SolutionThere is one circular current carrying loop. A charged particle is projected with a certain speed along the axis of the coil. How will the coil exert magnetic force on the charged particle?
View Solution
Knowledge Check
In a region of space, both electric and magnetic field are present simultaneously in opposite direction. A positively charged particle is projected with certain speed an angle θ(<90∘) with magnetic field. It will move in a
AHelicat path of uniform pitchBHelical path of increasing pitchCHelical path of decreasing pitchDHelical paht, whose pitch first decreases and then increasesAssertion: Magnetic field can always accelerate the charged particle, if it is not moving, parallel or antiparallel to the magnetic field.
Reason: When the velocity of a charged particle makes an angle other than 0∘ or 180∘ , magnetic force is nonzero.AIf both assertion and reason are correct and reason is a correct explanation of the assertion .BIf both assertion and reason are correct but reason is not the correct explanation of assertion.CIf assertion is correct but reason is incorrect.DIf assertion is incorrect but reason is correct.Four charged particles are projected perpendicularly into the magnetic field with equal velocity. Which will have minimum frequency of rotation?
AProtonBElectronCLi+DHe+0
A proton and an alpha particle projected with same velocity in uniform transverse magnetic field then
View SolutionWhen a charged particle is projected perpendicular to the magnetic field, the force acting on the charged particle is……………of the radius of circular path but…………….the speed of the charged particle.
View SolutionWhat is the path of a charged particle moving in a uniform magnetic field with initial velocity (i) parallel to the field? (ii) perpendicular to the field? (iii) at some angle with the direction of magnetic field.
View SolutionA charged particle is projected at a very high speed perpendicular to a uniform magnetic field . The particle will
View SolutionA: The magnetic field lines also represent the lines of force on a moving charged particle at every point.
R: Force on a moving charge acts parallel to the magnetic field.
View Solution