A proton and an alpha particle projected with same velocity in uniform transverse magnetic field then
Proton will have greater frequency than alpha particle
Alpha particle will have greater frequency than proton
Both the particles will have same frequency
Their frequencies cannot be compared
To solve the problem, we need to analyze the motion of a proton and an alpha particle in a uniform transverse magnetic field. The key points to consider are the charge and mass of the particles, as well as the frequency of their circular motion in the magnetic field.
1. Identify the Charges and Masses:
- The charge of a proton (qp) is +e, where e≈1.6×10−19C.
- The charge of an alpha particle (qα) is +2e (since it consists of 2 protons).
- The mass of a proton (mp) is approximately 1.67×10−27kg.
- The mass of an alpha particle (mα) is approximately 4mp (since it consists of 2 protons and 2 neutrons).
2. Determine the Radius of Circular Motion:
- The radius of the circular path in a magnetic field is given by the formula:
r=mvqB
- For the proton:
rp=mpvqpB
- For the alpha particle:
rα=mαvqαB
3. Calculate the Frequencies of Circular Motion:
- The frequency of circular motion in a magnetic field is given by:
f=qB2πm
- For the proton:
fp=qpB2πmp
- For the alpha particle:
fα=qαB2πmα
4. Substituting the Values:
- For the proton:
fp=eB2πmp
- For the alpha particle:
fα=2eB2π(4mp)=eB4πmp
5. Comparing Frequencies:
- Now we can compare fp and fα:
fp=eB2πmpandfα=eB4πmp
- Clearly, fp is greater than fα:
fp>fα
6. Conclusion:
- Therefore, the frequency of the proton is greater than that of the alpha particle when both are projected with the same velocity in a uniform transverse magnetic field.
Final Answer:
The proton will have a greater frequency than the alpha particle.
---
- The charge of a proton (qp) is +e, where e≈1.6×10−19C.
- The charge of an alpha particle (qα) is +2e (since it consists of 2 protons).
- The mass of a proton (mp) is approximately 1.67×10−27kg.
- The mass of an alpha particle (mα) is approximately 4mp (since it consists of 2 protons and 2 neutrons).
- The radius of the circular path in a magnetic field is given by the formula:
r=mvqB
- For the proton:
rp=mpvqpB
- For the alpha particle:
rα=mαvqαB
- The frequency of circular motion in a magnetic field is given by:
f=qB2πm
- For the proton:
fp=qpB2πmp
- For the alpha particle:
fα=qαB2πmα
- For the proton:
fp=eB2πmp
- For the alpha particle:
fα=2eB2π(4mp)=eB4πmp
- Now we can compare fp and fα:
fp=eB2πmpandfα=eB4πmp
- Clearly, fp is greater than fα:
fp>fα
- Therefore, the frequency of the proton is greater than that of the alpha particle when both are projected with the same velocity in a uniform transverse magnetic field.
The proton will have a greater frequency than the alpha particle.
Topper's Solved these Questions
Similar Questions
A proton and an α- particle is projected with equal kinetic energy in transverse uniform magnetic field B. The ratio of radii of proton to that of alpha particle is
View SolutionA proton, deutron and α particle are moving with same momentum in uniform magnetic field. The ratio of magnetic forces acting on them is___and their speed are in ratio____
View Solution
Knowledge Check
A proton an an α−particle, moving with the same velocity, enter a uniform magnetic field, acting normal to the plane of their motion. The ratio of the radii of the circular paths descirbed by the proton and α-particle is
A1:2B1:4C1:16D4:1A proton and an alpha particle are separately projected in a region where a uniform magnetic field exists. Their initial velocities are perpendicular to direction of magnetic field. If both the particles move around magnetic field in circles of equal radii, the ratio of momentum of proton to alpha particle (pppα) is
A1B12C2D14A proton, deutron and α particle are moving with same momentum in uniform magnetic field. The ratio of magnetic forces acting on them is___and their speed are in ratio____
A1:2:4and2:1:1B2:1:1and4:2:1C4:2:1and2:1:1D1:2:4and1:1:2
A proton an an α−particle, moving with the same velocity, enter a uniform magnetic field, acting normal to the plane of their motion. The ratio of the radii of the circular paths descirbed by the proton and α-particle is
View SolutionTwo charged particle M and N are projected with same velocity in a uniform magnetic field. Then M and N respectively.
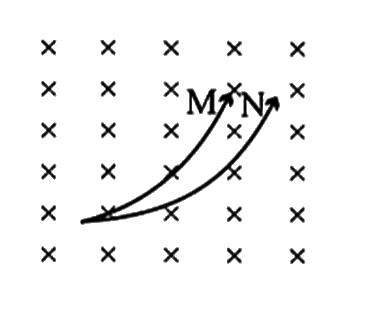
View SolutionAn electron and a proton are projected with same velocity perpendicular to a magnetic field.
(a) Which particle will describe the smaller circle?
(b) Which particle will have greater frequency?
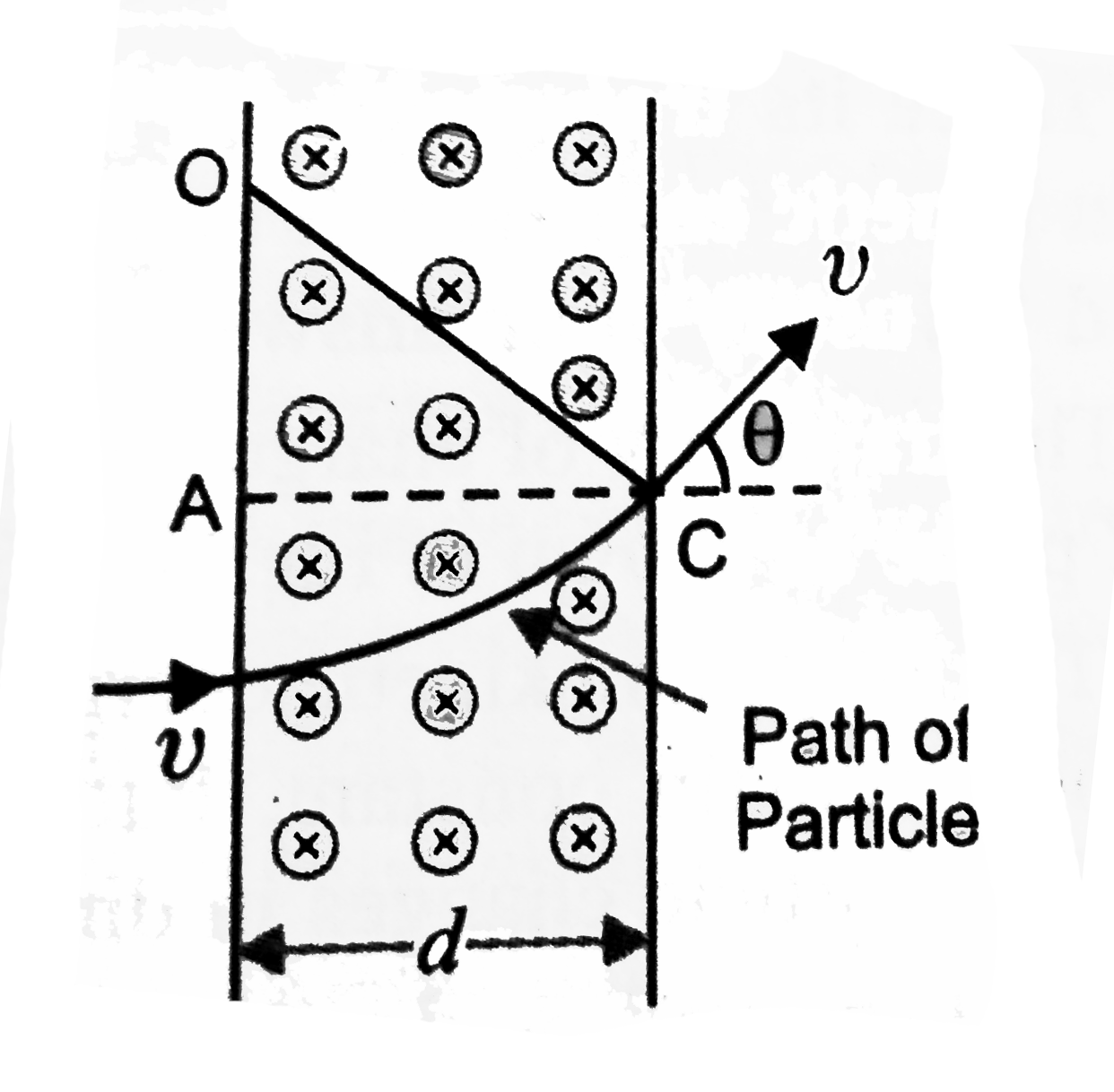
View SolutionA proton and an alpha particle are projected in a perpendicular magnetic field B which exists in a region of width d, figure. Find the ratio of the sines of angles of deviation suffered by the proton and the alpha particle if before entering the magnetic field both the particles (i) have the same momentum (ii) have the same kinetic energy.
View SolutionStatement-1: A proton and an α- particle are projected with the same kinetic energy at right angles to a uniform magnetic field, then the α-particle will move along a circular path of smaller radius than the proton.
Statement-2: Bqv=mv2r
View Solution
