Two long straight parallel wires A and B separated by a distance d, carry equal current I flowing in same direction as shown in the figure.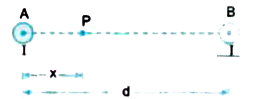 
(a) Find the magnetic field at a point P situated between them at a distance x from one wire.
(b) Show graphically the variation of the magnetic field with distance x for 0<x<d.
(a) Magnetic field at point due to current I in wire A, BA=μ0I2πx↑⏐
⏐⏐
and magnetic field due to current I in wire B, BB=μ0I2π(d−x)⏐⏐
⏐
⏐↓
Net magnetic field B=(BA−BB)↑⏐
⏐
⏐
⏐⏐=μ0I2π[1x−1(d−x)]
⇒B=μ0I2πd−2πx(d−x)↑⏐
⏐
⏐⏐
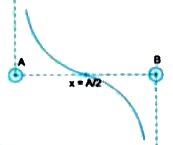
(b) Variation of magnetic field B with distance x is shown here.
For x=d2 magnetic field B=0. For x<d2 magnetic field B is directed upward and for x>d2 magnetic field B is directed downward.
Similar Questions
Two thin, long, parallel wires, separated by a distance 'd' carry a current of 'i' A in the same direction. They will
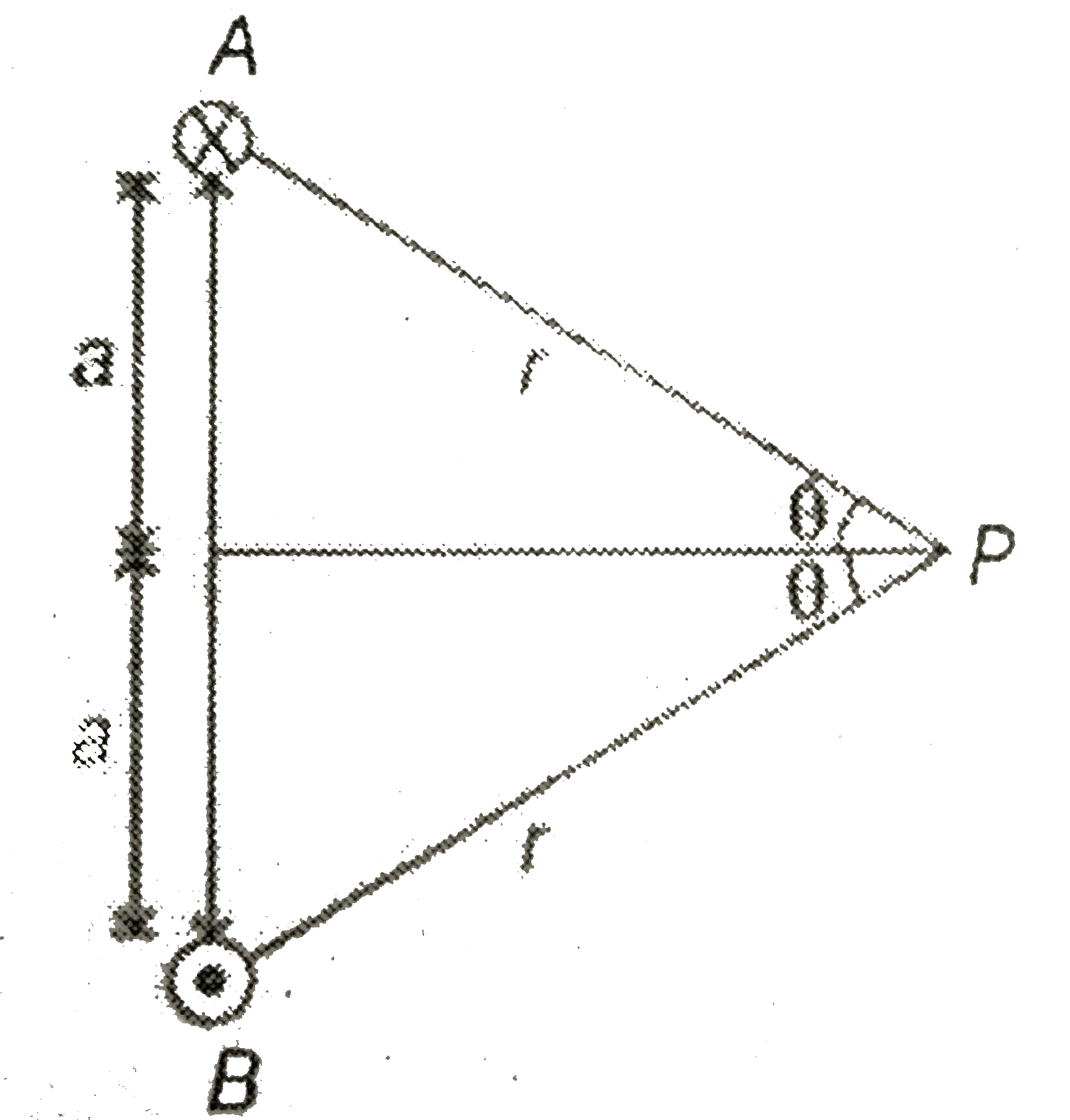
View SolutionTwo long parallel wire A and B situated perpendicuilar to the plane of the paper at a distance 2a are carrying equal currents I in opposite direction as show in the figure . The value of magnetic induction at point P situated at equal distance r from both the wires will be
View Solution
Knowledge Check
- Question 1 - Select One
Two thin, long, parallel wires, separated by a distance 'd' carry a current of 'i' A in the same direction. They will
Arepel each other with a force of μ0i2/(2πd)Battract each other with a force of μ0i2/(2πd)Crepel each other with a force of μ0i2/(2πd2)Dattract each other with a force of μ0i2/(2πd2) - Question 2 - Select One
Two long parallel wire A and B situated perpendicuilar to the plane of the paper at a distance 2a are carrying equal currents I in opposite direction as show in the figure . The value of magnetic induction at point P situated at equal distance r from both the wires will be
Aμ0la4πr2Bμ0la2πr2Cμ0laπr2Dμ0la√r2−a2πr2 - Question 3 - Select One
Two long parallel wires carry equal current I flowing in the same direction are at a distance 2d apart. The magnetic field B at a point lying on the perpendicular line joining the wires and at a distance x from the midpoint is
Aμ0idπ(d2+x2)Bμ0ixπ(d2−x2)Cμ0ix(d2+x2)Dμ0id(d2+x2)
Two long parallel wires carry equal current I flowing in the same direction are at a distance 2d apart. The magnetic field B at a point lying on the perpendicular line joining the wires and at a distance x from the midpoint is
View SolutionLet two long parallel wires, a distance d apart, carry equal currents I in the same direction. One wires at x=0, the other at x=d (as shown in Fig) Determine magnetic field at any point x-axis between the wires as a function of x.
View SolutionLet two long parallel wires, a distance d apart, carry equal currents I in the same direction. One wires at x=0, the other at x=d (as shown in Fig) Determine magnetic field at any point x-axis between the wires as a function of x.
View SolutionFigure shows two long, straight wires carrying electric currents in opposite directions. The separation between the wires is 5.0 cm. Find the magnetic field at a point P midway between the wires.
View SolutionTwo long parallel wires carry equal current I flowing in the same direction are at a distance 2d apart. The magnetic field B at a point lying on the perpendicular line joining the wires and at a distance x from the midpoint is
View Solution