Define the collections {E1,E2,E3,...} of ellipses and {R1,R2,R3,...} of rectangles as follows :
E1:x29+y24=1
R1: rectangle of largest area, with sides parallel to the axes, inscribed in E1,
Rn−1,n>1,
Rn : rectangle of largest area, with sides parallel to the axes, inscribed in En>1.
Then which of the following options is /are correct ?
the eccentricities of E18 and E19 are NOT equal.
The distance of a locus from the centre in E9is√532.
N∑n=1(area of Rn)<24, for each positive integer N.
The length of latusrectum of E9is16.
The correct Answer is:C, D
Given equation of ellipse
E1:x29+y24=1 ....(i)
Now, let a vertex of rectangle of largest area with sides parallel to the axes, incribed in E1 be (3cosθ,2sinθ).
So, area of rectangle R1=2(3cosθ)×2(2sinθ)=12sin(2θ)

The area of R1 will be maximum, if θ=π4 and maximum area is 12 square units and length of sides of rectangle R1 are 2acosθ=√2a=3√2= length of major axis of ellipse E1 and 2bsinθ=√2b=2√2= length of minor axis of ellipse E2.
So, E2:x2(a√2)2+y2(b√2)2=1 and maxsimum area of rectangle R2=2(a√2)(b√2)
So, En=x2⎛⎝a(√2)n−1⎞⎠2+y2⎛⎝b(√2)n−1⎞⎠2=1, and maximum area of rectangle Rn=2⎛⎜
⎜⎝a(√2)n−1⎞⎟
⎟⎠⎛⎜
⎜⎝b(√2)n−1⎞⎟
⎟⎠
Now option (a),
Since, eccentricity of ellipse En=en=
⎷1(bn)2(an)2
⎷1−⎛⎝b(√2)n−1⎞⎠2⎛⎝a(√2)n−1⎞⎠2=√1−b2a2=√1−45=√53
is independent of π,so eccentricity of E18andE19 are equal.
Option (b), Distance between focus and centre of E9=e.a9
=a(√28)(2)=324×√53=√516unit.
Option (c), ∵n∑n=1(area ofRn)<(area ofR1)+(ara ofR2)+.....∞
<2ab+2ab2+2ab22+......
<2ab(1+12+122+......)
<12(11−1/2)
⇒N∑n=1(area ofRn)<24, each of positive integer N.
Option (d), Length of latusrectum E9=2b29a9=2b2a(√2)8
=2×43×16=16 units.
Hence, option (c) and (d) are correct.
Topper's Solved these Questions
- SOLVED PAPER 2019BOOK - IIT JEE PREVIOUS YEARCHAPTER - SOLVED PAPER 2019EXERCISE - Paper -1 section-3
6 Videos
- SOLVED PAPER 2019BOOK - IIT JEE PREVIOUS YEARCHAPTER - SOLVED PAPER 2019EXERCISE - Paper -2 section-1
8 Videos
- SOLVED PAPER 2019BOOK - IIT JEE PREVIOUS YEARCHAPTER - SOLVED PAPER 2019EXERCISE - Paper -2 section-3
4 Videos
- SEQUENCES AND SERIESBOOK - IIT JEE PREVIOUS YEARCHAPTER - SEQUENCES AND SERIESEXERCISE - RELATION BETWEEN AM,GM, HM AND SOME SPECIAL SERIES
34 Videos
- STRAIGHT LINE AND PAIR OF STRAIGHT LINESBOOK - IIT JEE PREVIOUS YEARCHAPTER - STRAIGHT LINE AND PAIR OF STRAIGHT LINESEXERCISE - GENERAL EQUATION OF PAIR OF STRAIGHT LINES (Objective Questions I) (Only one correct option)
1 Videos
Similar Questions
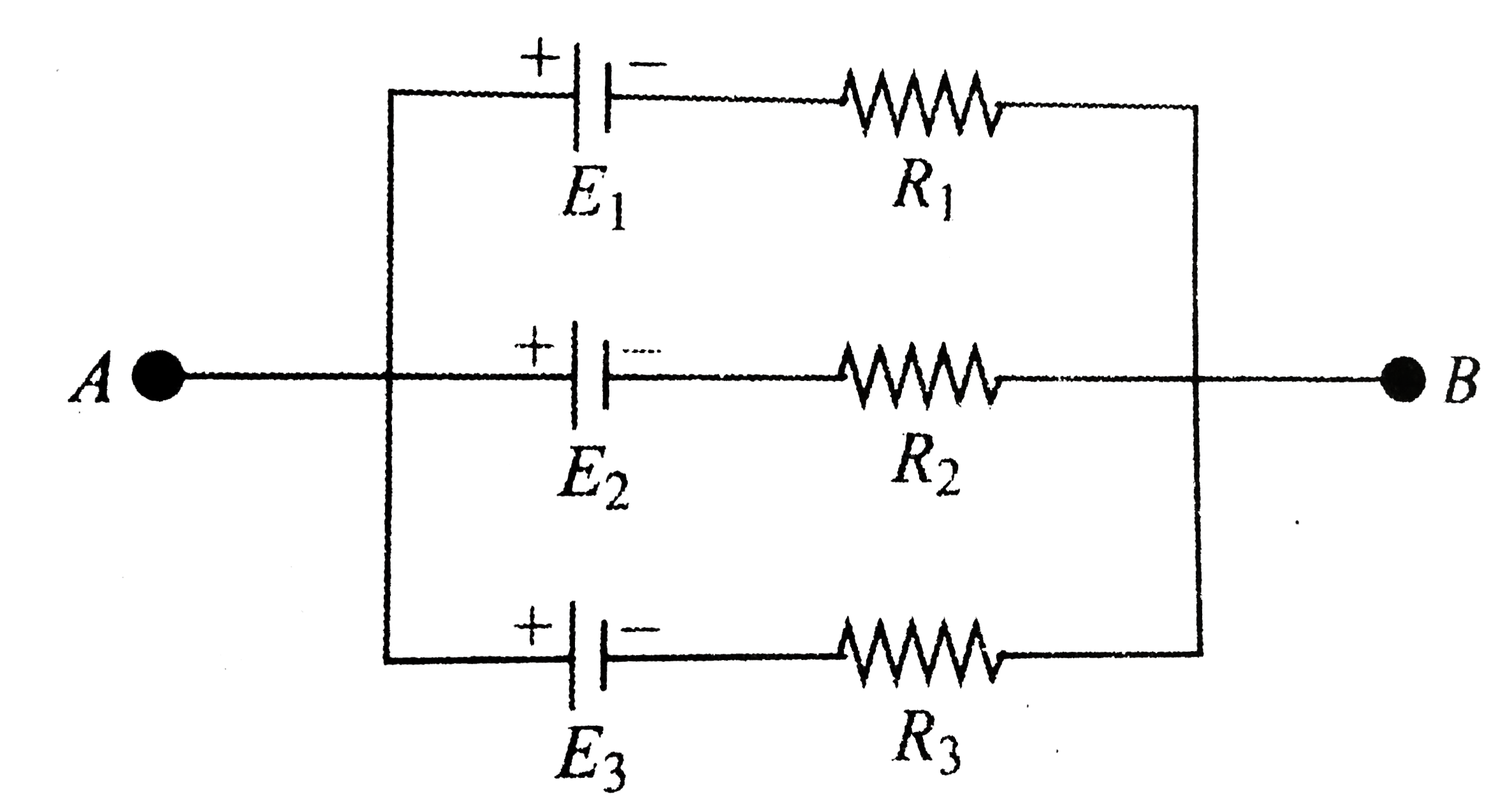
For the batteries shown in fig. R1,R2andR3 are the internal resistance of E1,E2,andE3, respectively Then, which of the following is / are correct?
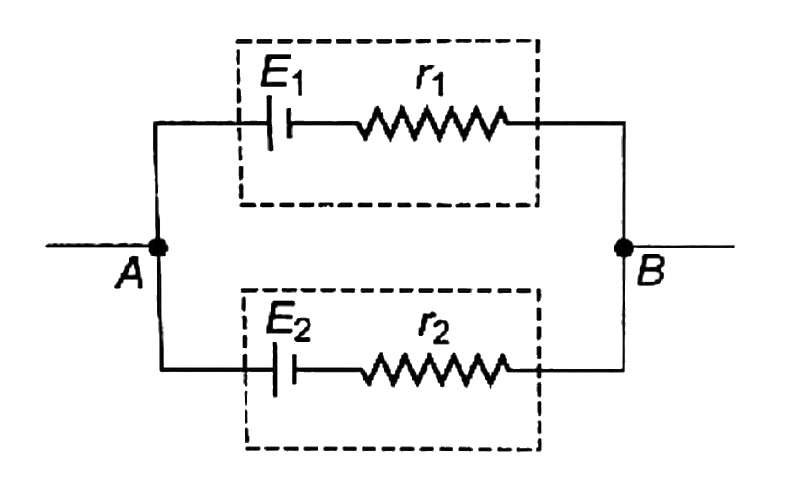
View SolutionTwo batteries of emf E1 and E2(E2>E1) and internal resistance r1 and r2 respectively are connected in parallel as shown in the figure. Then, which of the followings statements is correct ?
View Solution
Knowledge Check
Define the collection {E1,E2,E3,.....} of ellipses and {R1,R2,R3,.....} of rectangles as follows:
E1=x29+y24=1 ,
R1 : rectangle of largest area, with sides parallel to the axes, inscribed in E1 ,
En : ellipse x2a2n+y2b2n=1 of largest are inscribed in Rn−1,n>1.
then which of the following options is/are corrct?AN∑n=1( area of Rn)<24, for each positive integer NBThe distance of a focus from the centre in E9 is √532CThe eccentricities of E18 and E19 are NOT equalDThe length of latus rectum of E9 is 16For the batteries shown in fig. R1,R2andR3 are the internal resistance of E1,E2,andE3, respectively Then, which of the following is / are correct?
 AThe equivalent internal resistance R of the system is given by (R1R2R3)/(R1R2+R2R3+R3R1).BIf E3=(E1R2+E2R1)/(R1+R2), the equivalent emf of the batteries will be equal to E3CThe equivalent emf to the battery is equal to E=(E1+E2+E3)/3DThe equivalent emf of the battery not only depends upon values of E1,E2,andE3 but also depends upon values of R1,R2andR3.
AThe equivalent internal resistance R of the system is given by (R1R2R3)/(R1R2+R2R3+R3R1).BIf E3=(E1R2+E2R1)/(R1+R2), the equivalent emf of the batteries will be equal to E3CThe equivalent emf to the battery is equal to E=(E1+E2+E3)/3DThe equivalent emf of the battery not only depends upon values of E1,E2,andE3 but also depends upon values of R1,R2andR3.Equation of ellipse E1 is x29+y24=1, A rectangle R1, whose sides are parallel to co-ordinate axes is inscribed in E1 such that its area is maximum now En is an ellipse inside Rn−1 such that its axes is along co-ordinate axes and has maxmim possible area ∀n≥2,n∈N, further Rn is a rectangle whose sides are parallel to co-ordinate axes and is inscribed in En−1. Having maximum area ∀n≥2,n∈N
Am∑n=1 area of rectangle (Rn)<24∀m∈NBLength of latus rectum of E9=16CDistance between focus and centre of E9=√532DThe eccentricities of E18 and E19 are not equal.
Two batteries of emf E1 and E2(E2>E1) and internal resistance r1 and r2 respectively are connected in parallel as shown in the figure. Then, which of the followings statements is correct ?

View SolutionThe ellipse E1:x29+y24=1 is inscribed in a rectangle R whose sides are parallel to the coordinates axes. Another ellipse E2 passing through the point (0, 4) circumscribes the rectangle R. The length (in units) of the major axis of ellipse E2 is
View SolutionThe ellipse E1:x29+y24=1 is inscribed in a rectangle R whose sides are parallel to the coordinate axes. Another ellipse E2 passing through the point (0, 4) circumscribes the rectangle R. The eccentricity of the ellipse E2 is √22 (b) √32 (c) 12 (d) 34
View SolutionThe ellipse E1:x29+y24=1 is inscribed in a rectangle R whose sides are parallel to the coordinate axes. Another ellipse E2 passing through the point (0, 4) circumscribes the rectangle R. The eccentricity of the ellipse E2 is √22 (b) √32 (c) 12 (d) 34
View SolutionLet E1andE2 denotes gravitational field at distance r1andr2 from the axis of an infinitely long solid cylinder of the radius R. Which of the following must hold true ?
View Solution
