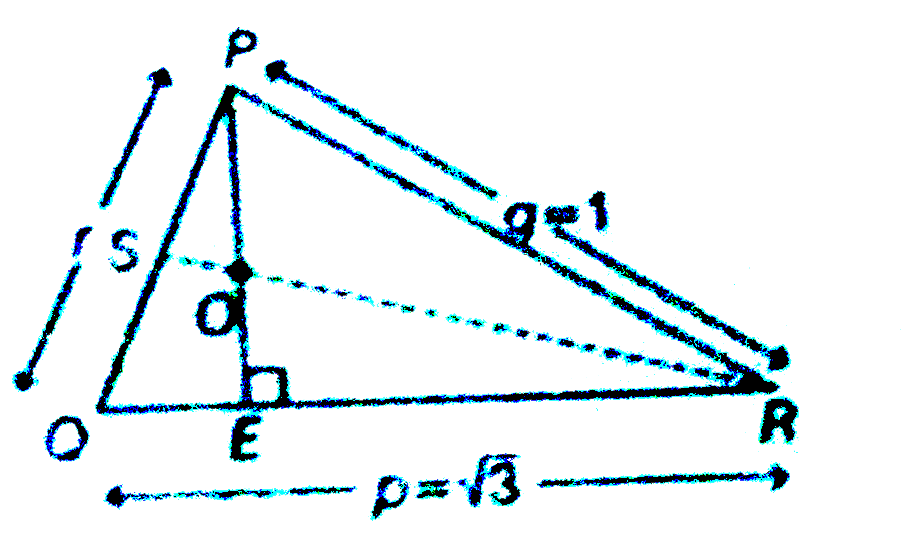
In a non-right -angled triangle $Δ P Q R$ , let p,q,r denote the lengths of the sides opposite to the angles at P,Q,R respectively. The median from R meets the side PQ at S, the perpendicular from P meets the side QR at E, and RS and PE intersect at O. if $p = \sqrt{3}, q = 1$ ,and the radius of the circumcircle of the $Δ P Q R$ equals 1, then which of the following options is/are correct ?

A

Length of $O E = \frac{1}{6}$

B

Length of $R S = \frac{\sqrt{7}}{2}$

C

Area of $Δ S O E = \frac{\sqrt{3}}{2}$

D

Radius of incircle of $Δ P R Q = \frac{\sqrt{3}}{2} (2 - \sqrt{3})$

Text Solution

Verified by Experts

The correct Answer is:A, B, D

Let a non- right angled $Δ P Q R$ ,Now, by sine rule.

$\frac{P}{sin P} = \frac{q}{sin Q} = \frac{r}{sin R} = 2 \times$ circumradius
$\Rightarrow \frac{\sqrt{3}}{sin P} = \frac{1}{sin Q} = \frac{r}{sin R} = 2 \times 1 [cirumradius =1 unit]$
$\Rightarrow sin P = \frac{\sqrt{3}}{2} and sin Q = \frac{1}{2}$
$\Rightarrow P = 120^{\circ} and Q = 30^{\circ}$ ( $∵ Δ P Q R$ is non -right angled triangle)
So, $R = 30^{\circ}$
$\Rightarrow = 1$ , so $Δ P Q R$ is an isoceles triangle. And, sinces RS and PE are the median of $Δ P Q R$ , so 'O' is centroid of the $Δ P Q R$ .
Now,
Option (a), From Apollonitus therorem,
$2 (P E^{2} + Q E^{2}) = P Q^{2} + P R^{2} + P R^{2} \Rightarrow 2 (P E^{2} + \frac{3}{4}) = 1 + 1$
$\Rightarrow P E^{2} = 1 - \frac{3}{4} \Rightarrow P E^{2} = \frac{1}{4} \Rightarrow P E = \frac{1}{2} units$
and $O E = \frac{1}{3} P E = \frac{1}{6} units [∵ O divides P E i s 2 : 1]$
Option (b) ,
Again from Apollonius theorem,
$2 (P S^{2} + R S^{2}) = P R^{2} + Q R^{2} \Rightarrow 2 (\frac{1}{4} + R S^{2}) = 1 + 3$
$\Rightarrow R S^{2} = 2 - \frac{1}{4} \Rightarrow R S^{2} = \frac{7}{4} \Rightarrow R S = \frac{\sqrt{7}}{2} units$
Option (c),
Area of $Δ S O E = \frac{1}{2} (O E) (S T)$
$= \frac{1}{2} \times \frac{1}{6} [(P S) {sin 60}^{\circ}]$
$= \frac{1}{12} \times \frac{1}{2} \times \frac{\sqrt{3}}{2}$
$= \frac{\sqrt{3}}{48}$ square units.
Option (d),
$∵ Inradius of Δ P Q R = \frac{Δ}{s} = \frac{\frac{1}{2} p q sin R}{\frac{1}{2} (p + q + r)} = \frac{\frac{1}{2} (\sqrt{3}) (1) \frac{1}{2}}{\frac{1}{2} (\sqrt{3} + 1 + 1)}$
$= \frac{\sqrt{3}}{2} (2 - \sqrt{3}) units$
Hence, options (a), (b) and (d) are correct.

|

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One or More
In a non right angled triangle $Δ P Q R$ , let $p, q, r$ denote the lengths of the sides opposite to the angle P,Q,R respectively. The median from R meets the side PQ at S, the perpendicular from P meets the side QR at E, and RS and PE intersect at O. if $p = \sqrt{3}, q = 1$ and the radius of the circumcircle of the $Δ P Q R$ equals to 1, then which of the followign options is/are correct?
Alength of $R S = \frac{\sqrt{7}}{2}$
Blength of $O E = \frac{1}{6}$
CRadius of incircle of $Δ P Q R = \frac{\sqrt{3}}{2} (2 - \sqrt{3})$
DArea of $Δ S O E = \frac{\sqrt{3}}{12}$
Question 2 - Select One
Let PQR be a triangle of $!$ area with a = 2 , b = $\frac{7}{2}$ and c = $\frac{5}{2}$ , where a , b and c are the lengths of the sides of the triangle opposite to the angles P , Q and R respectively. Then , $\frac{2 sin P - sin 2 P}{2 sin P + sin P}$ equals
A $\frac{3}{4 Δ}$
B $\frac{45}{4 Δ}$
C ${(\frac{3}{4 Δ})}^{2}$
D ${(\frac{45}{4 Δ})}^{2}$
Question 3 - Select One
Let PQR be a triangle of area $Δ$ with $a = 2, b = 7 / 2$ , and $c = 5 / 2$ , where a, b and c are the lengths of the sides of the triangle opposite to the angles at P, Q and R, respectively. Then $\frac{2 sin P - sin 2 P}{2 sin P + sin 2 P}$ equals
A $\frac{3}{4 Δ}$
B $\frac{45}{4 Δ}$
C ${(\frac{3}{4 Δ})}^{2}$
D ${(\frac{45}{4 Δ})}^{2}$

IIT JEE PREVIOUS YEAR-SOLVED PAPER 2019-Paper -1 section-2

Home
Ask Doubt
Profile