A boy whose eye level is $1.3 m$ from the ground, spots a balloon moving with the wind in a horizontal line at same height from the ground. The angle of elevation of the balloon from the eyes of the boy at an instant is $60^{\circ}$ . After 2 seconds, the angle of elevation reduces to $30^{\circ}$ . If the speed of the wind is $29 \sqrt{3} m / s$ then find the height of the balloon from the ground.

Video Solution

Text Solution

Verified by Experts

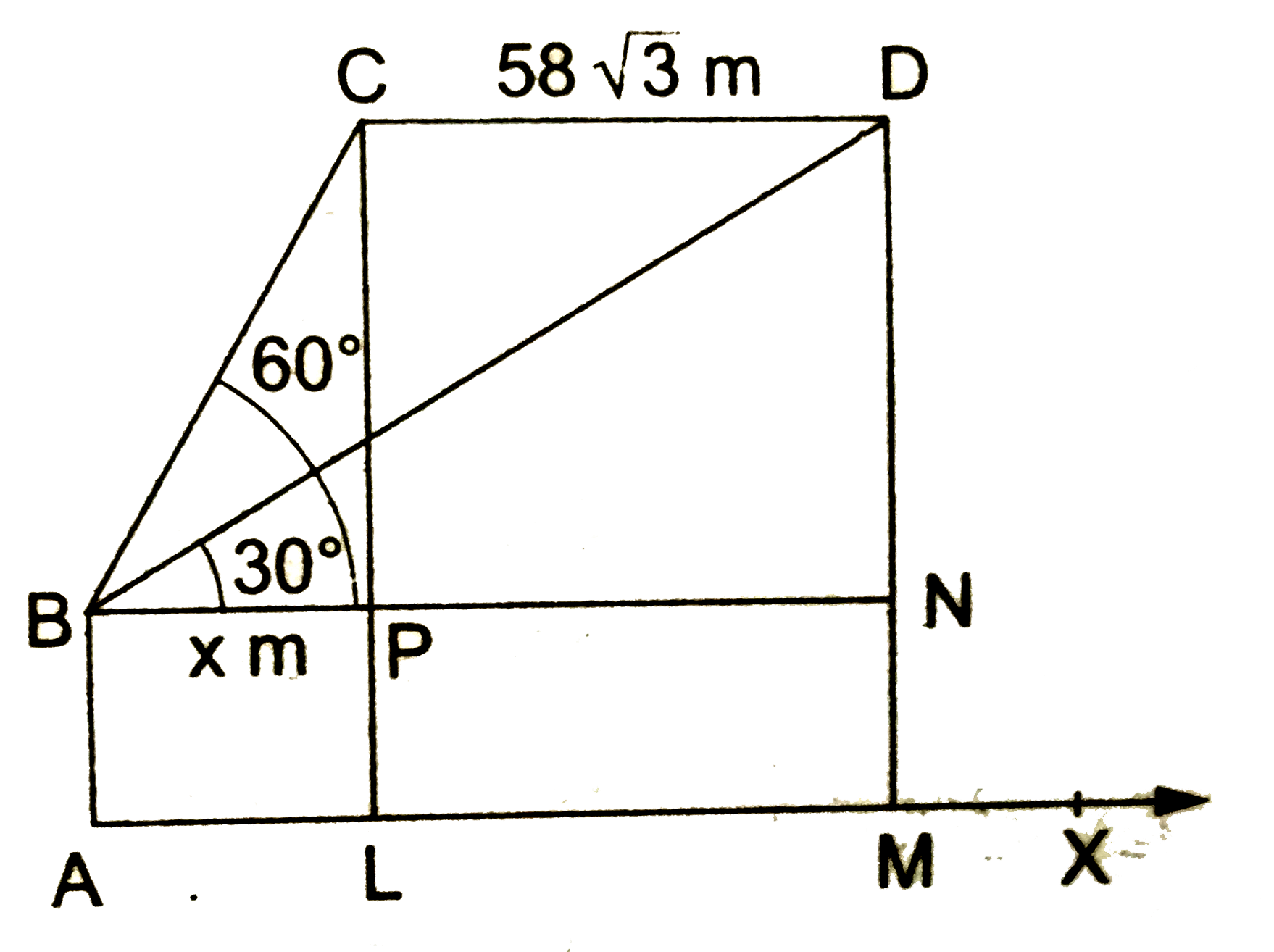
Let AB be the position of the boy and AX be the the horizontal grund. Let C and D be the two positions of the ballon. Draw $C L ⊥ A X, D M ⊥ A X$ and $B N ⊥ D M$ , intersecting CL at P. Then $∠ C B N = 60^{\circ}$ and $∠ D B N = 30^{\circ}$ .
Distance covered by the balloon in 2 seconds.
$= (29 \sqrt{3} \times 2) m = 58 \sqrt{3} m$ .
$∵ C D = 58 \sqrt{3}$ .
Let $B P = x$ metres, Then,
$B N = (B P + P N) = (B P + C D) = (x + 58 \sqrt{3}) m and D N = C P$ From right $Δ B N D$ , we have
$\frac{D N}{B N} = {tan 30}^{\circ} = \frac{1}{\sqrt{3}}$ .
$\Rightarrow \frac{D N}{(x + 58 \sqrt{3}) m} = \frac{1}{\sqrt{3}} \Rightarrow D N = \frac{(x + 58 \sqrt{3})}{\sqrt{3}} m ........ (i)$
From right $Δ B P C$ , we have
$\frac{C P}{B P} = {tan 60}^{\circ} = \sqrt{3}$
$\Rightarrow \frac{C P}{x m} = \sqrt{3} \Rightarrow C P = (x \sqrt{3})$
$\Rightarrow (3 x - x) = 58 \sqrt{3} \Rightarrow 2 x = 58 \sqrt{3} \Rightarrow x = 29 \sqrt{3}$ .
From (ii), we get
$C P = (29 \sqrt{3} \times \sqrt{3}) m = (29 \times 3) m = 87 m$
$∴$ height of the ballon from the ground.
$= C L = C P + P L = C P + A B = 87 m + 1.3 m = 88.3 m$
Hence, the height of the balloon from the ground is $88.3$ metres.

Updated on:21/07/2023

The angle of elevation of an airplane from a point on the ground is $60^{\circ}$ . After a flight of $30$ seconds, the angle of elevation becomes $30^{\circ}$ . If the airplane is flying at a constant height of $3000 \sqrt{3}$ m, find the speed of the airplane.
A $200 m / s$
B $250 m / s$
C $350 m / s$
D $300 m / s$
The angle of elevation of an aeroplane from a point on the ground is $60^{\circ}$ .After flying for 30 seconds ,the angle of elevation changes to $30^{\circ}$ .If the aeroplane is flying at a height of $1500 \sqrt{3}$ metre , then what is the speed (in m/s) of aeroplane?
A50
B100
C200
D300
The angle of elevation of the top of a tower at a point G on the ground is $30^{\circ}$ . On walking 20 m towards the tower the angle of elevation becomes $60^{\circ}$ . The height of the tower is equal to :
A $10 / \sqrt{3} m$
B $20 \sqrt{3} m$
C $20 / \sqrt{3} m$
D $10 \sqrt{3} m$