An electrician has to repair an electric fault on a pole of height 4m. He needs to reach a point 1.3m below the top of the pole to undertake the repair work. What should be the length of the ladder that he should use which when inclined at an angle of 60o to the horizontal would enable him to reach the required position?
The correct Answer is:(i) 3.46m , (ii) 40m , (iii) 20m
Let AB be the electric pole such that AB = 4 m . Let C be a point 1m below B.
Then, AC=4m−1m=3m.
Let OC be the ladder.Then, ∠AOC=60∘
Let OC = x metres.
From right ΔOAC, we have
OCAC=cosec60∘⇒x3=2√3⇒x=6√3×√3√3=2√3.
⇒x=(2×1.73)=3.46
Hence the length of the ladder is 3.46m.
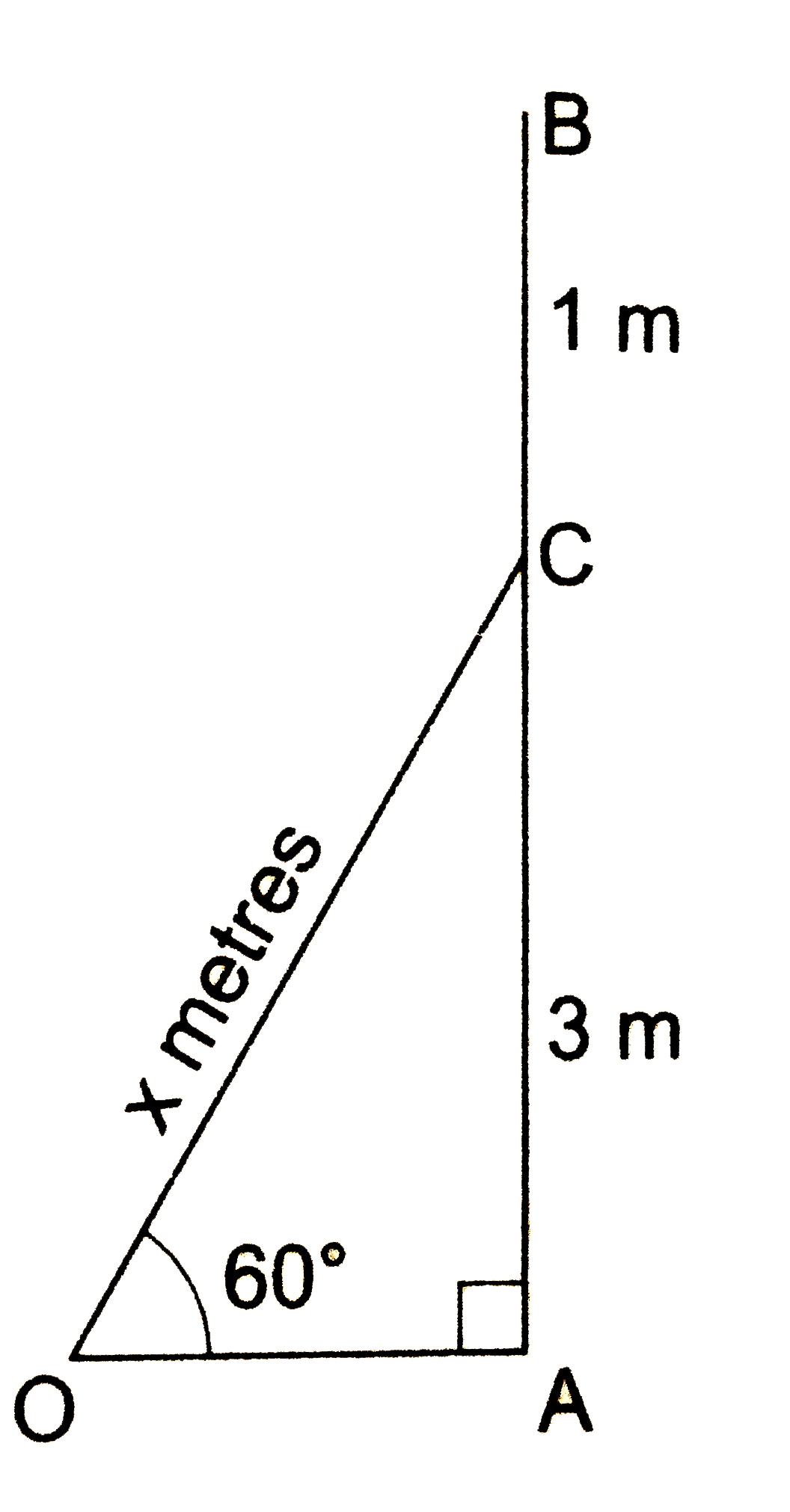
Topper's Solved these Questions
- HEIGHTS AND DISTANCESBOOK - RS AGGARWALCHAPTER - HEIGHTS AND DISTANCESEXERCISE - Multiple Choice Questions (Mcq)
25 Videos
- HEIGHTS AND DISTANCESBOOK - RS AGGARWALCHAPTER - HEIGHTS AND DISTANCESEXERCISE - Multiple Choice Questions (Mcq)
25 Videos
- COORDINATE GEOMETRYBOOK - RS AGGARWALCHAPTER - COORDINATE GEOMETRYEXERCISE - Multiple Choice Questions (Mcq)
34 Videos
- LINEAR EQUATIONS IN TWO VARIABLES BOOK - RS AGGARWALCHAPTER - LINEAR EQUATIONS IN TWO VARIABLES EXERCISE - QUESTION
2 Videos
Similar Questions
An electrician has to repair an electric fault on a pole of height 5 m. She needs to reach a point 1.3m below the top of the pole to undertake the repair work. What should be the length of the ladder that she should use which, when inclined at
View SolutionAn electrician has to repair an electric fault on a pole of height 4 metres.He needs to reach a point 1 m below the top of the pole to undertake the repair work.What should be the length of the ladder that he should use, which when inclined at an angle 60∘ to the horizontal would enable him to reach the required position? [use √3=1.73]
View Solution
Knowledge Check
A person of height 2m wants to get a fruit which is on a pole of height (103)m. If he stands at a distance (4√3)m from the foot of the pole, then the angle at which he should throw the stone, so that it hits the fruit is
A60∘B45∘C90∘D30∘A person of height 2m wants to get a fruit which is on a pole of height (103)m. If he stands at a distance (4√3)m from the foot of the pole, then the angle at which he should throw the stone, so that it hits the fruit is
A60∘B45∘C90∘D30∘Ravi is 113 times as fast as Pradeep. If Pradeep has a head start of 50 m then what should be the length of the racecourse such that both of them reach the finishing point at the same time ?
A250 mB100 mC150 mD200 m
Anjali in an electrician and she has to repair an electric fault on a pole of height 5 m. She needs to reach to a point on the pole of 1.3 m below the top of the pole to undertake the repair work. What should be the length of the ladder that she should use which, when inclined at angle of 60° from the horizontal, would enable her to reach the required position? Further, how far from the foot of the pole should she place the foot of the ladder? What value is indicated from the question?
View SolutionA contractor plans to install two slides for the children to play in a park. For the children below the age of 5 years, she prefers to have a slide whose top is at a height of 1.5 m, and is inclined at an angle of 30∘to the ground, whereas for elder children, she wants to have a steep slide at a height of 3m, and inclined at an angle of 60∘ to the ground. What should be the length of the slide in each case?
View SolutionA particle of mass m is suspended from a string of length l fixed to the point O. What velocity should be imparted to the particle in its lowermost position so that the string is just able to reach the horizontal diameter of the circle?
View SolutionA monkey wants to climb up a pole of 50 metre height. He first climbs up 1 metre but he falls back by the same height. Again he climbs up 2 metre but he falls back by 1 metre. Once again he climbs up 3 metre but he falls back by 1 metre. Again he climbs up 4 metre but he falls back be 1 metre. In this way he reaches at the top of the pole. If it is known that the monkey needs 10 seconds for 1 metre in upward direction , then the total time required by monkey to reach at the top of the pole. For your kind information it must be clear to you that when he will reach on the top, he will not be slip back. The total time required by this monkey to reach on the top of the poll is:
View SolutionA monkey wants to climb up a pole of 50 metre height. He first climbs up 1 metre but he falls back by the same height. Again he climbs up 2 metre but he falls back by 1 metre. Once again he climbs up 3 metre but he falls back by 1 metre. Again he climbs up 4 metre but he falls back be 1 metre. In this way he reaches at the top of the pole. If it is known that the monkey needs 10 seconds for 1 metre in upward direction , then the total time required by monkey to reach at the top of the pole. For your kind information it must be clear to you that when he will reach on the top, he will not be slip back. The total time required by this monkey to reach on the top of the poll is:
View Solution
