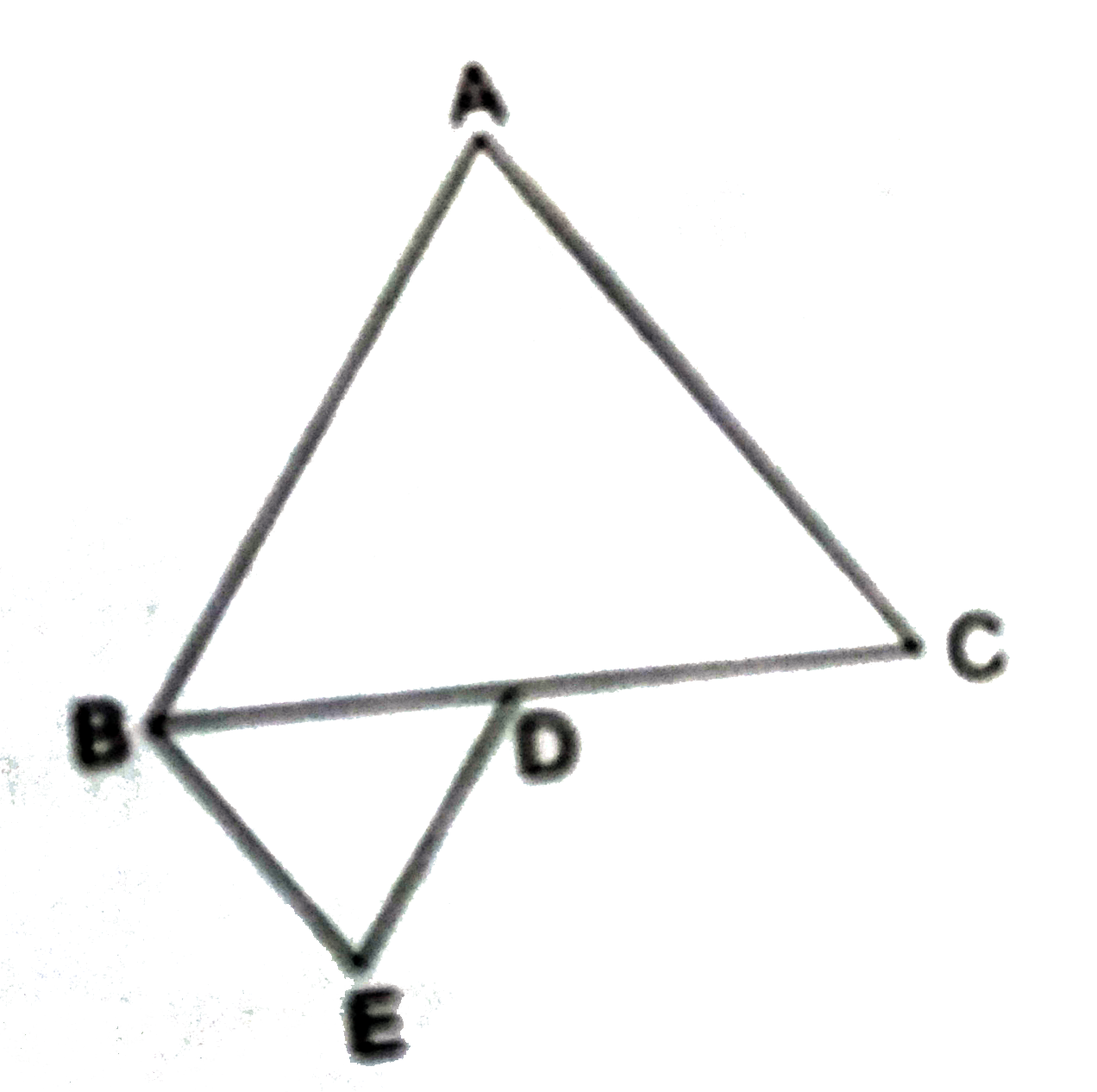
ABC and BDE are two equilateral triangles such that D is the mid-point of BC . The ratio of the areas of the triangles ABC and BDE is 2:1 (b) 1:2 (c) 4:1 (d) 1:4
1:2
2:1
1:4
4:1
The correct Answer is:D
ΔABC~ΔBDE [ ∴ both are equilateral]
Also, BD=12BC=12AB [ ∴ D is the midpoint of BC]
Now, ar(ΔABC)ar(ΔBDE)=AB2BD2=AB2(12AB)2=41
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - MULTPILE-CHOICE QUESTIONS (MCQ) ( MATCHING OF COLUMNS)1videos
TRIANGLES
- BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - Test Yourself20videos
TRIANGLES
- BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - Exercise 7E30videos
TRIANGLES
- BOOK - RS AGGARWALCHAPTER - T-RATIOS OF SOME PARTICULAR ANGLESEXERCISE - Exercise 1127videos
T-RATIOS OF SOME PARTICULAR ANGLES
- BOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC IDENTITIESEXERCISE - Test Yourself20videos
TRIGONOMETRIC IDENTITIES
Similar Questions
ABC and BDE are two equilateral triangles such that D is the mid-point of BC . The ratio of the areas of the triangles ABC and BDE is 2:1 (b) 1:2 (c) 4:1 (d) 1:4
View SolutionTick the correct answer and justify:ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Ratio of the areas of triangles ABC and BDE is
(A) 2:1 (B) 1:2 (C) 4:1 (D) 1:4View SolutionIn Figure, ABCandBDE are two equilateral triangles such that D is the mid-point of BC,AE intersects BC in F
Prove that: ar(BDE)=12ar(BAE)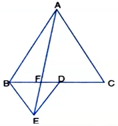
View SolutionIf D,E and F are the mid-points of the sides of a △ABC, the ratio of the areas of the triangles DEF and DCE is (a) 1.1:1 (b) 1:1.1 (c) 1:1 (d) 0.9:1
View SolutionIn Figure, ABCandBDE are two equilateral triangles such that D is the mid-point of BC,AE intersects BC in F
Prove that: ar(BDE)=14ar(ABC)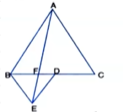
View SolutionIn Figure, ABCandBDE are two equilateral triangles such that D is the mid-point of BC,AE intersects BC in F
Prove that: ar(BFE)=ar(AFD)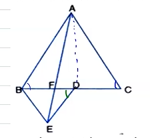
View SolutionIn Figure, ABCandBDE are two equilateral triangles such that D is the mid-point of BC,AE intersects BC in F Prove that: ar(FED)=18ar(AFC)
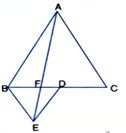View SolutionIn Figure, ABC and BDE are two equilateral triangls such that D is the mid-point of BC.AE intersects BC in F. Prove that: ar ( BFE)= 2 ar (EFD)
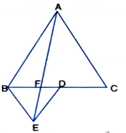View SolutionABCD is a square. E is the mid-point of BC and F is the mid-point of CD . The ratio of the area of triangle AEF to the area of the square ABCD is (a) 1 : 2 (b) 1 : 3 (c) 1 : 4 (d) 3 : 8
View SolutionThe ratio of the areas of the incircle and circumcircle of an equilateral triangle is (a) 1 : 2 (b) 1 : 3 (c) 1 : 4 (d) 1 : 9
View Solution