A bullet of mass m travelling with a speed v hits a block of mass M initially at rest and gets embedded in it. The combined system is free to move and there is no other force acting on the system. The heat generated in the process will be
zero
mv22
Mmv22(M−m)
mMv22(M+m)
The correct Answer is:D
To solve the problem of finding the heat generated when a bullet of mass m traveling with speed v hits a block of mass M that is initially at rest and gets embedded in it, we can follow these steps:
Step 1: Understand the System
We have a bullet of mass m moving with velocity v colliding with a stationary block of mass M. After the collision, the bullet gets embedded in the block, and they move together with a common velocity V′.
Step 2: Apply Conservation of Momentum
Since there are no external forces acting on the system, we can apply the conservation of momentum principle:
Initial Momentum=Final Momentum
The initial momentum before the collision is:
pinitial=mv+0=mv
The final momentum after the collision (when both the bullet and block move together) is:
pfinal=(M+m)V′
Setting the initial momentum equal to the final momentum gives us:
mv=(M+m)V′
Step 3: Solve for the Final Velocity V′
From the equation above, we can solve for V′:
V′=mvM+m
Step 4: Calculate Initial and Final Kinetic Energy
Next, we need to calculate the initial and final kinetic energy of the system.
- Initial Kinetic Energy (KEinitial):
Only the bullet is moving initially, so:
KEinitial=12mv2
- Final Kinetic Energy (KEfinal):
After the collision, both the bullet and the block move together with velocity V′:
KEfinal=12(M+m)(V′)2
Substituting V′ from Step 3:
KEfinal=12(M+m)(mvM+m)2
Step 5: Simplify the Final Kinetic Energy
Now, simplifying KEfinal:
KEfinal=12(M+m)⋅m2v2(M+m)2
This simplifies to:
KEfinal=12⋅m2v2M+m
Step 6: Calculate the Heat Generated
The heat generated (Q) in the process is equal to the change in kinetic energy:
Q=KEinitial−KEfinal
Substituting the values we calculated:
Q=12mv2−12⋅m2v2M+m
Factoring out 12v2:
Q=12v2(m−m2M+m)
Step 7: Simplify Further
To simplify the expression inside the parentheses:
Q=12v2(m(M+m)−m2M+m)
This simplifies to:
Q=12v2(mMM+m)
Final Answer
Thus, the heat generated in the process is:
Q=12mMv2M+m
We have a bullet of mass m moving with velocity v colliding with a stationary block of mass M. After the collision, the bullet gets embedded in the block, and they move together with a common velocity V′.
Since there are no external forces acting on the system, we can apply the conservation of momentum principle:
From the equation above, we can solve for V′:
Next, we need to calculate the initial and final kinetic energy of the system.
Only the bullet is moving initially, so:
After the collision, both the bullet and the block move together with velocity V′:
Now, simplifying KEfinal:
The heat generated (Q) in the process is equal to the change in kinetic energy:
To simplify the expression inside the parentheses:
Thus, the heat generated in the process is:
Topper's Solved these Questions
- LAWS OF MOTION BOOK - MTG-WBJEECHAPTER - LAWS OF MOTION EXERCISE - WB JEE PREVIOUS YEARS QUESTIONS (CATEGORY 2: SINGLE OPTION CORRECT TYPE (2 MARKS))
1 Videos
- LAWS OF MOTION BOOK - MTG-WBJEECHAPTER - LAWS OF MOTION EXERCISE - WB JEE PREVIOUS YEARS QUESTIONS (CATEGORY 3: ONE OR MORE THAN ONE OPTION CORRECT TYPE (2 MARKS))
2 Videos
- LAWS OF MOTION BOOK - MTG-WBJEECHAPTER - LAWS OF MOTION EXERCISE - WB JEE WORKOUT (CATEGORY 3: ONE OR MORE THAN ONE OPTION CORRECT TYPE (2 MARKS))
10 Videos
- KINETIC THEORY OF GASES BOOK - MTG-WBJEECHAPTER - KINETIC THEORY OF GASES EXERCISE - WB JEE PREVIOUS YEARS QUESTIONS (MCQ)
7 Videos
- MAGNETIC EFFECT OF CURRENTBOOK - MTG-WBJEECHAPTER - MAGNETIC EFFECT OF CURRENTEXERCISE - WB JEE Previous Years Questions
22 Videos
Similar Questions
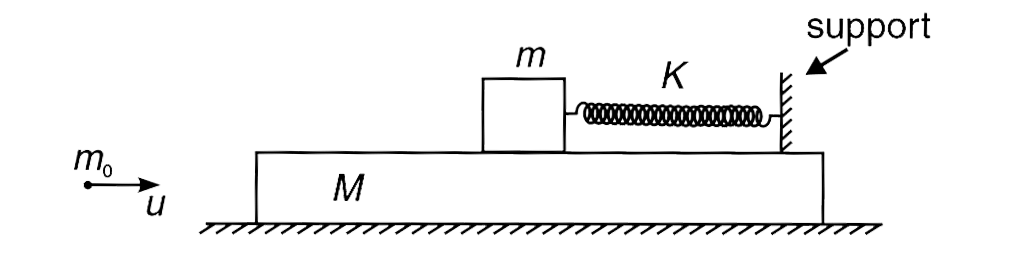
In the system shown in fig. block of mass M is placed on a smooth horizontal surface. There is a mass less rigid support attached to the block. Block of mass m is placed on the first block and it is connected to the support with a spring of force constant K. There is no friction between the blocks. A bullet of mass m0, moving with speed u hits the block of mass M and gets embedded into it. The collision is instantaneous. Assuming that m always stays over M, calculate the maximum extension in the spring caused during the subsequent motion.
K=8960N/m,u=400m/s
View SolutionA bullet of mass m strikes a block of mass M. The bullet remains embedded in the block. Find the amplitude of the resulting SHM.

View Solution
Knowledge Check
A bullet of mass in travelling with a speed v hits a block of mass M initially at rest and gets embedded in it. The combined system is free to move and there is no other force acting on the system. The heat generated in the process will be
AzeroBmv22CMmv22(M−m)DmMv22(M+m)A bullet of mass m moving with a speed v strikes a wooden block of mass M & gets embedded into the block. The final speed is
A√MM+nVB√mM+nVCmM+nVDV2A bullet of mass m moving with velocity v strikes a block of mass M at rest and gets embedded into it. The kinetic energy of the composite block will be
A12mv2×m(m+M)B12mv2×M(m+M)C12mv2×(M+m)mD12Mv2×m(m+M)
A bullet of mass m moving with velocity v strikes a block of mass M at rest and gets embedded into it. The kinetic energy of the composite block will be
View SolutionA 50 g bullet moving with velocity 10 m / s strikes a block of mass 950 g at rest and gets embedded in it. The loss in kinetic energy will be
View SolutionA 50 g bullet moving with velocity 10 m / s strikes a block of mass 950 g at rest and gets embedded in it. The loss in kinetic energy will be
View SolutionA bullet of mass 'x' moves with a velocity y, hits a wooden block of mass z at rest and gets embedded in it. After collision, the wooden block and bullet moves with a velocity
View SolutionA wooden block of mass M rests on a horizontal surface. A bullet of mass m moving in the horizontal direction strikes and gets embedded in it. The combined system covers a distance x on the surface. If the coefficient of friction between wood and the surface is μ , the speed of the bullet at the time of striking the block is (where m is mass of the bullet)
View Solution
