A projectile thrown with an initial velocity of 10ms−1 at an angle with the horizontal, has a range of 5 m. Taking g=10 ms−2 and neglecting air resistance, what will be the estimated value of α ?
15∘
30∘
45∘
75∘
The correct Answer is:A, D
To find the angle of projection (α) for a projectile thrown with an initial velocity of 10 m/s that has a range of 5 m, we can use the range formula for projectile motion. The formula for the range (R) of a projectile is given by:
R=u2sin(2α)g
Where:
- R = Range of the projectile
- u = Initial velocity
- g = Acceleration due to gravity
- α = Angle of projection
Step 1: Substitute the known values into the range formula
Given:
- R=5m
- u=10m/s
- g=10m/s2
Substituting these values into the range formula:
5=(10)2sin(2α)10
Step 2: Simplify the equation
We can simplify the equation:
5=100sin(2α)10
This simplifies to:
5=10sin(2α)
Step 3: Solve for sin(2α)
Now, we can isolate sin(2α):
sin(2α)=510=12
Step 4: Determine the angles corresponding to sin(2α)=12
The angles for which the sine function equals 12 are:
2α=30∘or2α=150∘
Step 5: Solve for α
Now, we can find α:
1. From 2α=30∘:
α=30∘2=15∘
2. From 2α=150∘:
α=150∘2=75∘
Conclusion
The estimated values of α are:
α=15∘orα=75∘
- R = Range of the projectile
- u = Initial velocity
- g = Acceleration due to gravity
- α = Angle of projection
Given:
- R=5m
- u=10m/s
- g=10m/s2
We can simplify the equation:
Now, we can isolate sin(2α):
The angles for which the sine function equals 12 are:
Now, we can find α:
α=30∘2=15∘
α=150∘2=75∘
The estimated values of α are:
Topper's Solved these Questions
- BOOK - MTG-WBJEECHAPTER - LAWS OF MOTION EXERCISE - WB JEE PREVIOUS YEARS QUESTIONS (CATEGORY 2: SINGLE OPTION CORRECT TYPE (2 MARKS))1videos
LAWS OF MOTION
- BOOK - MTG-WBJEECHAPTER - KINETIC THEORY OF GASES EXERCISE - WB JEE PREVIOUS YEARS QUESTIONS (MCQ)7videos
KINETIC THEORY OF GASES
- BOOK - MTG-WBJEECHAPTER - MAGNETIC EFFECT OF CURRENTEXERCISE - WB JEE Previous Years Questions22videos
MAGNETIC EFFECT OF CURRENT
Similar Questions
A projectile is thrown with a velocity of 10ms^(-1) at an angle of 30o with horizontal.The value of maximum height gained by it is (a) 1m(b) 1.25m (c) 2m
View SolutionA body is project at t= 0 with a velocity 10ms−1 at an angle of 60∘ with the horizontal .The readius of curvature of its trajectory at t=1s is R. Neglecting air resitance and taking acceleration due to gravity g=10ms−2, the value of R is :
View Solution
Knowledge Check
- Question 1 - Select One
A projectile is thrown with initial velocity u0 and angle 30∘ with the horizontal. If it remains in the air for 1s. What was its initial velocity ?
A19.6ms−1B9.8ms−1C4.9ms−1D1ms−1 - Question 2 - Select One
A particle is projected with velocity of 10ms at an angle of 15° with horizontal.The horizontal range will be(g=10ms2)
A10mB5mC2.5mD1m - Question 3 - Select One
A projectile is thrown with a velocity of 10ms−1 at an angle of 60∘ with horizontal. The interval between the moments when speed is √5gm/s is (Take, g=10ms−2)
A1sB3sC2sD4s
A particle is thrown with a velocity 10m/s and its horizontal range is 5m. Find angle/angles of the projection.
View SolutionA body is projected at 45∘ with a velocity of 20ms−1 has a range of 30m .The decrease in range due to air resistance is?(g=10ms−2)
View SolutionA particle is thrown at time t = 0 with a velocity of 10ms−1 at an angle 60∘ with the horizontal from a point on an inclined plane, making an angle of 30∘ with the horizontal. The time when the velocity of the projectile becomes parallel to the incline is
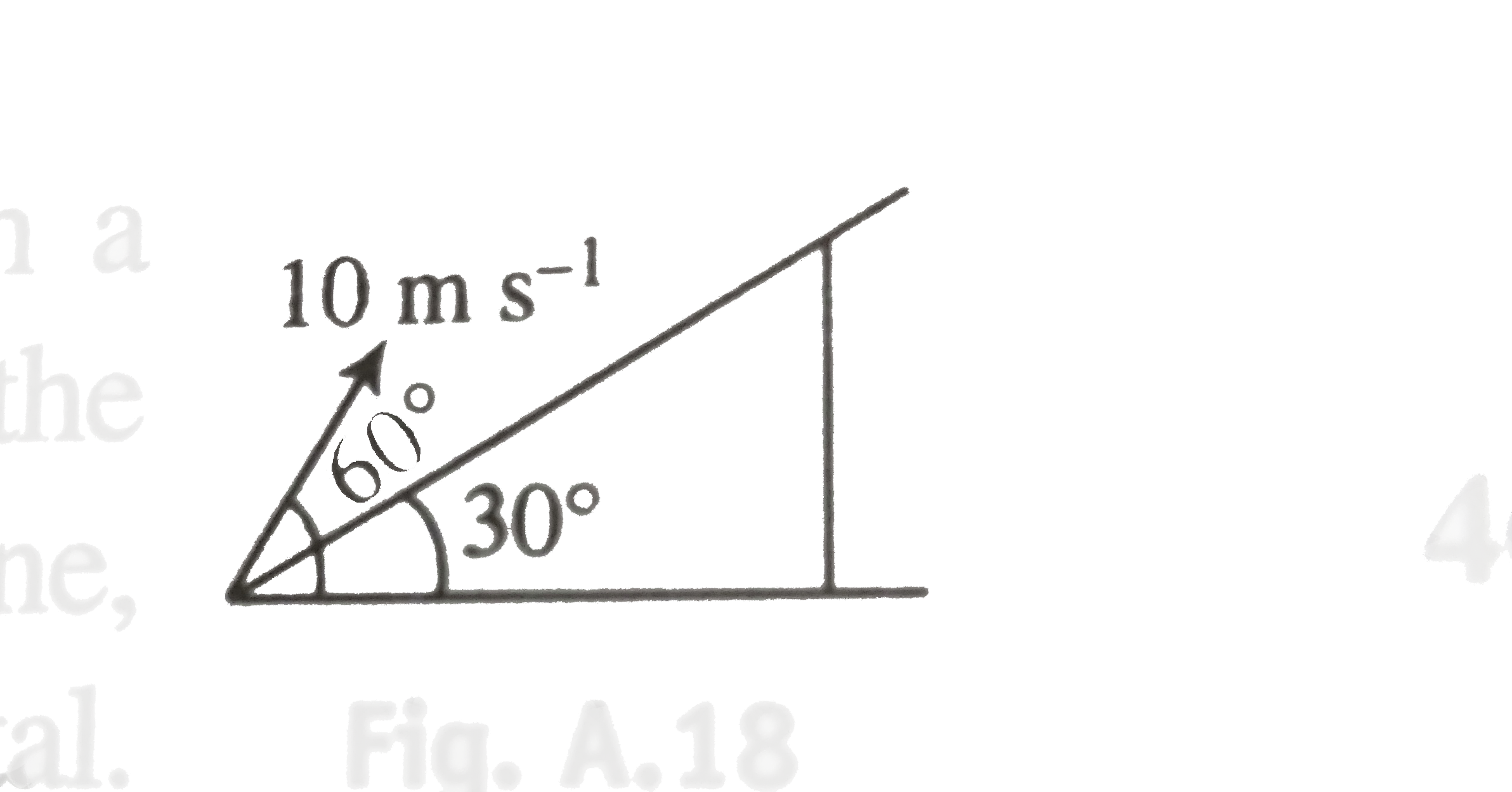 View Solution
View SolutionA projectile is projected with the initial velocity (6i+8j)m/s. The horizontal range is (g=10m/s2)
View SolutionThe maximum height attained by a ball projected with speed 20ms−1 at an angle 45∘ with the horizontal is [take g = 10ms−2]
View Solution

