A small spherical body of radius r and density $ρ$ moves with the terminal velocity v in a fluid of coefficient of viscosity $η$ and density $σ$ . What will be the net force on the body?

$\frac{4 π}{3} r^{3} (ρ - σ) g$

$6 π η r v$

infinity

Text Solution

Verified by Experts

The correct Answer is:C

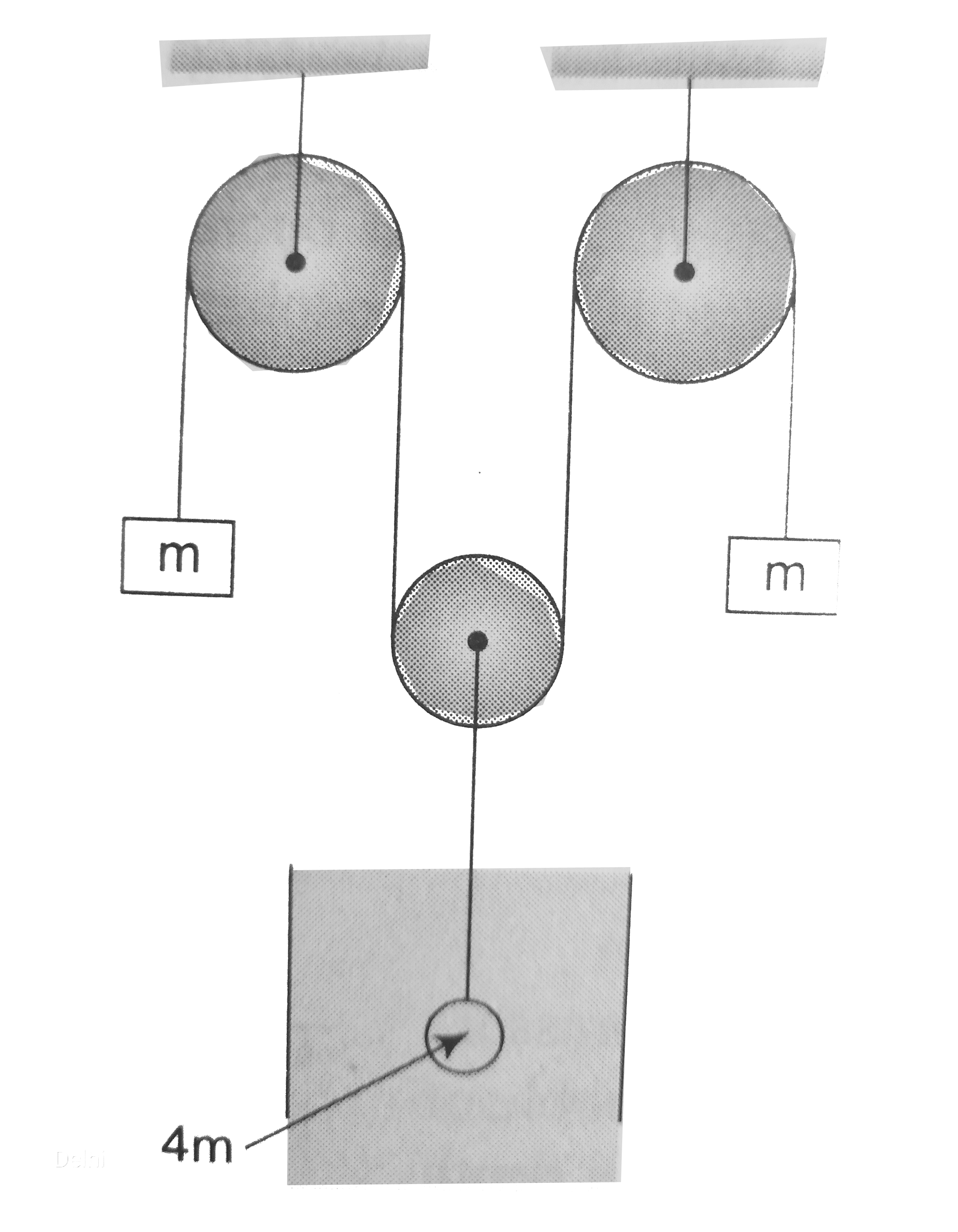
A spherical ball of mass 4m, density $σ$ and radius $r$ is attached to a pulley-mass system as shown in figure. The ball is released in a liquid of coefficient of viscosity $η$ and density $ρ (< \frac{σ}{2})$ . If the length of the liquid column is sufficiently long, the terminal velocity attained by the ball is given by (assume all pulleys to be massless and string as massless and inextensible):
A $\frac{2}{9} \frac{r^{2} (2 σ - ρ) g}{η}$
B $\frac{2}{9} \frac{r^{2} (σ - 2 ρ) g}{η}$
C $\frac{2}{9} \frac{r^{2} (σ - 4 ρ) g}{η}$
D $\frac{2}{9} \frac{r^{2} (σ - 3 ρ) g}{η}$
A drop of water of radius $r$ is falling rhough the air of coefficient of viscosity $η$ with a constant velocity of $v$ the resultant force on the drop is
A $\frac{1}{6 π η r v}$
B $6 π η r v$
C $\sqrt{6 π η r v}$
Dzero
The terminal velocity v of a small steel ball ofradius r fal ling under gravity through a column ofa viscous liquid of coefficient of viscosity $η$ depends on mass of the ball m, acceleration due to gravity g, coefficient of viscosity $η$ and radius r. Which of the following relations is dimensionally correct?
A $v_{r} \propto \frac{η m g}{r}$
B $v_{r} \propto \frac{m g r}{η}$
C $v_{r} \propto \frac{m g}{r η}$
D $v_{r} \propto m g η r$