Question

Interference of light is based on the superposition principle according to which at a particular point in the medium the resultant displacement produced by two or more light waves is the vector sum of the displacement produced by the two individual light waves.
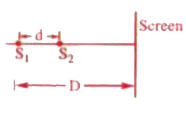
A British physicist Thomas Young made two pin holes $S_1\text{and}{S}_2$, separated by a very very small distance 'd' on an opaque screen which were illuminated by another pin hole S lit by a monochromatic source of light. so $S_1\text{and}{S}_2$ behaves as two coherent sources of light. spherical waves emanating from $S_1\text{and}{S}_2$ produce interference fringes on the screen AB. if P be a point situated at a distance x from central point O of the screen, then path difference between the waves coming from the two sources is
$S_{2}P-S_{1}P=\frac{xd}{D}$
Bright fringe is obtained on the screen if path difference $\frac{xd}{D}$ is an integer multiple of wavelength $\lambda$. However, we get a dark fringe on the screen if the path difference is an odd multiple of $\frac{\lambda }{2}$.
Q. Will the central point O on the screen be bright or dark?

Explanation

The central point O is bright because path difference `S_(2)O-S_(1)O` is zero and the two waves reach in same phase there.