In an experiment on photoelectric effect, the slope of the cut-offf voltage versus frequency of incident light is found to be 4.12×10−15V s. calculate the value of Planck's constant.
As per Einstein.s photoelectric equation, slope of V0−v graph is he=4.12×10−15V s
∴Planck.s constant h=4.12×10−15×e=4.12×10−15×1.6×10−19=5.59×10−34Js.
Topper's Solved these Questions
- DUAL NATURE OF RADIATION AND MATTERBOOK - U-LIKE SERIESCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - ADDITIONAL EXERCISES
15 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - U-LIKE SERIESCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - CASE BASED/SOURCE-BASED INTEGRATED QUESTIONS
10 Videos
- CURRENT ELECTRICITY BOOK - U-LIKE SERIESCHAPTER - CURRENT ELECTRICITY EXERCISE - SELF ASSESSMENT TEST (SECTION C )
3 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - U-LIKE SERIESCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - SELF ASSESSMENT TEST (SECTION-B) (VERY SHORT ANSWER QUESTIONS)
4 Videos
Similar Questions
In an experiment on photoelectric effect, the slope of the cut off voltage versus frequency of incident light is found to be 4.12×10−15Vs. Given e=1.6×10−19C, estimate the value of Planck's constant.
View SolutionIn an experiment on photoelectric effect, the slope of the cut off voltage versus frequency of incident light is found to be 4.12×10−15Vs. Given e=1.6×10−19C, estimate the value of Planck's constant.
View Solution
Knowledge Check
In an experiment on the photoelectric effect , the slope of the cut - off voltage versus frequency of incident light is found to be 4.12×10−15V s . The value of Planck's constant is
A6.592×10−34 J sB6.592×10−31 J sC9.592×10−34 J sD6.592×10−30 J sIn photoelectric effect the slope of stop of stopping potential versus frequency of incident light for a given surface will be
Ahe−1Be hCeDhFor a photoelectric cell, the graph shown the variation of cut off voltage (V0) with frequency (v) of incident light is
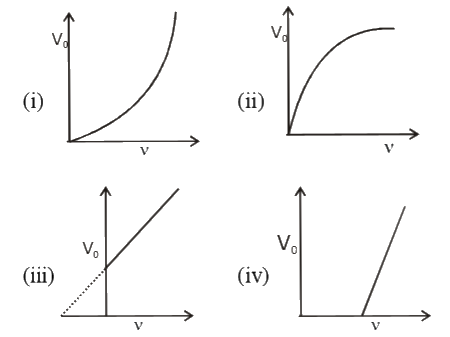 A(i)B(ii)C(iii)D(iv)
A(i)B(ii)C(iii)D(iv)
In photoelectric effect the slope of stop of stopping potential versus frequency of incident light for a given surface will be
View SolutionIn photoelectric effect the slope of straight line graph between stopping potential (Vs) and frequency of incident light (v) gives

View SolutionIn photoelectric effect the slope of straight line graph between stopping potential (Vs) and frequency of incident light (v) gives

View SolutionIn photo electric effect, the slope of the straight line graph between stopping potential and frequency of the incident light gives the ratio of Planck's constant to
View SolutionIn photoelectric effect experiment, the slope of the graph of the stopping potential versus frequency gives the value of :
View Solution
