In ΔABC if ∠BAC=90∘ and AB=AC, then ∠ABC is
30∘
60∘
45∘
25∘
The correct Answer is:C
To solve the problem, we need to analyze the given information about triangle ABC:
1. Given Information:
- Angle BAC = 90 degrees (∠BAC = 90°)
- AB = AC (The sides opposite to angles ABC and ACB are equal)
2. Understanding the Triangle:
Since AB = AC, triangle ABC is an isosceles triangle with the right angle at A.
3. Using the Triangle Sum Property:
The sum of the angles in any triangle is 180 degrees. Therefore, we can write the equation:
∠ABC+∠ACB+∠BAC=180°
Substituting the known values:
∠ABC+∠ACB+90°=180°
4. Simplifying the Equation:
To find the sum of angles ABC and ACB, we can rearrange the equation:
∠ABC+∠ACB=180°−90°=90°
5. Setting the Angles Equal:
Since AB = AC, the angles opposite these sides (∠ABC and ∠ACB) must be equal. Let's denote these angles as x:
∠ABC=xand∠ACB=x
Therefore, we can write:
x+x=90°
This simplifies to:
2x=90°
6. Solving for x:
Dividing both sides by 2 gives:
x=90°2=45°
7. Conclusion:
Thus, the measure of angle ABC (∠ABC) is 45 degrees.
Final Answer:
∠ABC=45°
- Angle BAC = 90 degrees (∠BAC = 90°)
- AB = AC (The sides opposite to angles ABC and ACB are equal)
Since AB = AC, triangle ABC is an isosceles triangle with the right angle at A.
The sum of the angles in any triangle is 180 degrees. Therefore, we can write the equation:
∠ABC+∠ACB+∠BAC=180°
Substituting the known values:
∠ABC+∠ACB+90°=180°
To find the sum of angles ABC and ACB, we can rearrange the equation:
∠ABC+∠ACB=180°−90°=90°
Since AB = AC, the angles opposite these sides (∠ABC and ∠ACB) must be equal. Let's denote these angles as x:
∠ABC=xand∠ACB=x
Therefore, we can write:
x+x=90°
This simplifies to:
2x=90°
Dividing both sides by 2 gives:
x=90°2=45°
Thus, the measure of angle ABC (∠ABC) is 45 degrees.
∠ABC=45°
Similar Questions
Knowledge Check
- Question 1 - Select One
If In ΔABC,∠ABC=5∠ACBand ∠BAC=3∠ACB, then ∠ABC=?
A130∘B80∘C100∘D120∘ - Question 2 - Select One
In ΔABC,∠BAC=90∘ and AB=12BC. Then the measure of ∠ACB is :
A60∘B30∘C45∘D15∘ - Question 3 - Select One
If ABC is an isosceles triangle with ∠C=90∘ and AC=5 cm, then AB is:
A5 cmB10 cmC5√2cmD2.5 cm
In triangle ABC , ∠BAC=90∘ and AB=AC. Seg AP is perpendicular to side BC. D is any point on side BC. Prove that 2(AD)2=(BD)2+(CD)2
View SolutionIn an isosceles ΔABC if ∠A=90∘ and AB=AC, find ∠B and ∠C.
View SolutionIn ΔABC,AC=BC and ∠BAC=70∘. Find ∠BCA
View SolutionIn right ΔABC, ∠B=90∘, AB=3cm and AC=6cm. Find ∠A.
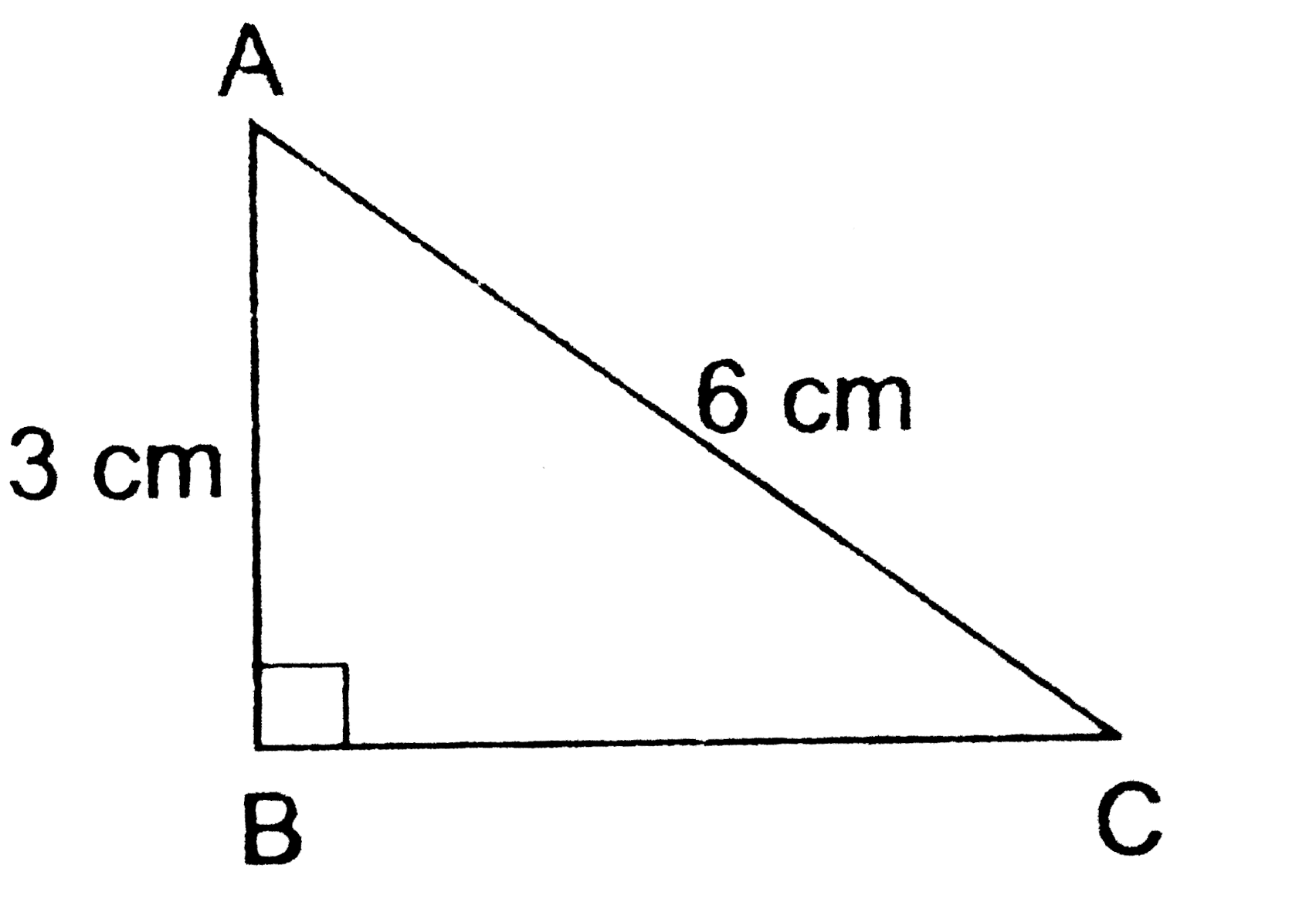 View Solution
View SolutionIn ΔABC, D and E are two mid points of sides AB and AC respec tively. If ∠BAC=40∘ and ∠ABC=65∘ then ∠CEDis
View Solution

