Let $θ, ϕ \in [0, 2 π]$ be such that $2 cos θ (1 - sin ϕ) = {sin}^{2} θ ((tan) \frac{θ}{2} + (cot) \frac{θ}{2}) cos ϕ - 1, tan (2 π - θ) > 0 and - 1 < sin θ < - \frac{\sqrt{3}}{2} .$ Then $ϕ$ cannot satisfy

A

$0 < ϕ < \frac{π}{2}$

B

$\frac{π}{2} < ϕ < \frac{4 π}{2}$

C

$\frac{4 π}{3} < ϕ < \frac{3 π}{2}$

D

$\frac{3 π}{2} < ϕ < 2 π$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:(a,c,d)

PLAN It is based on range of sin x, i.e.
$[- 1, 1]$ and the internal for $a < x < b$ .
Desription of Situtaion As $θ, ϕ \in [0, 2 π]$ and
$tan (2 π - θ) > 0, - 1 sin θ < - \frac{\sqrt{3}}{2}$
$tan (2 π - θ) > 0$
$\Rightarrow - tan θ > 0$
$∴ θ \in II or IV quadrant.$
Also, $- 1 < sin θ - \frac{\sqrt{3}}{2}$

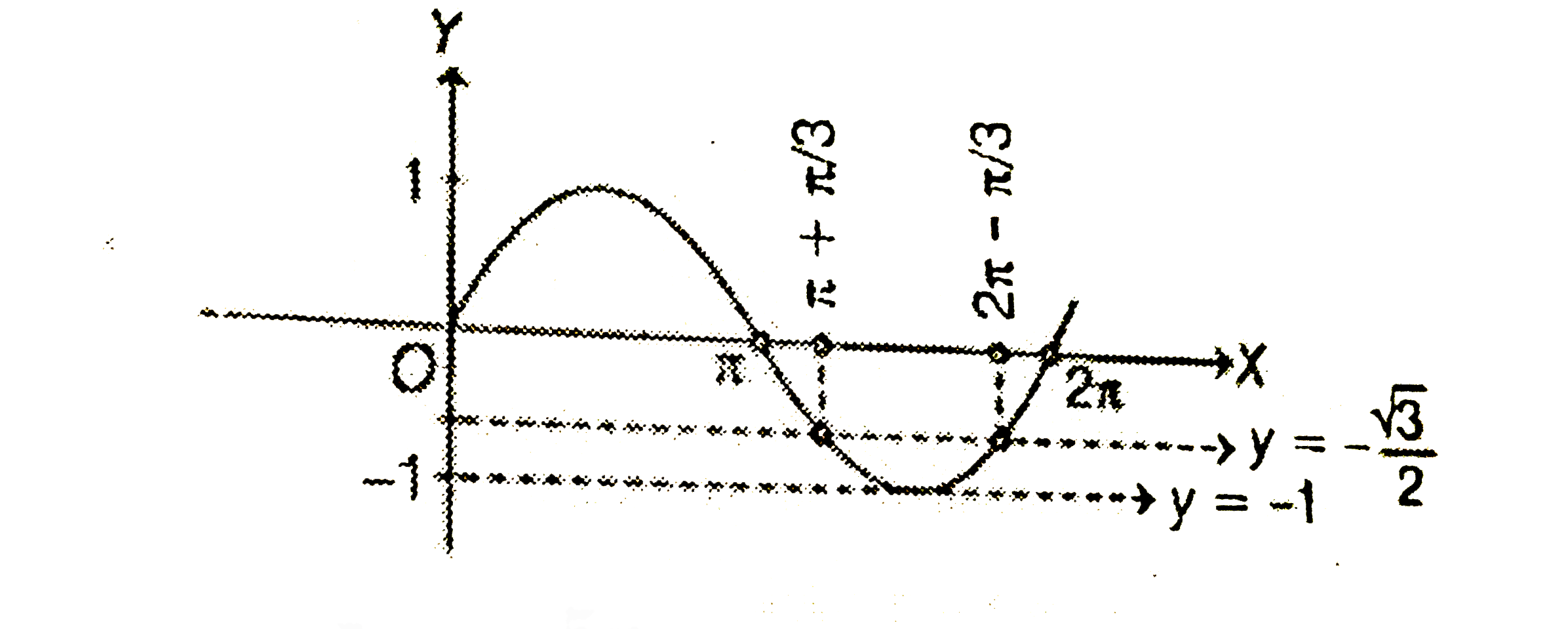
$\Rightarrow \frac{4 π}{3} < θ < \frac{5 π}{3} but θ \in II or IV quadrant$
$\Rightarrow \frac{3 π}{2} < θ < \frac{5 π}{3} ... (i)$
Here, $2 cos θ (1 - sin ϕ) = {sin}^{2} θ (tan \frac{θ}{2} + cot \frac{θ}{2}) cos ϕ - 1$
$\Rightarrow 2 cos θ - 2 cos θ sin ϕ = {sin}^{2} θ ⎛ ⎝ \frac{{sin}^{2} \frac{θ}{2} + {cos}^{2} \frac{θ}{2}}{sin \frac{θ}{2} cos \frac{θ}{2}} ⎞ ⎠ cos ϕ - 1$
$\Rightarrow 2 cos θ - 2 cos θ ϕ = 2 {sin}^{2} θ (\frac{1}{sin θ}) cos ϕ - 1$
$\Rightarrow 2 cos θ + 1 = 2 sin ϕ cos θ + 2 sin θ cos ϕ$
$\Rightarrow 2 cos θ + 1 = 2 sin (θ + ϕ) ... (i i)$
From Eq. (i), $\frac{3 π}{2} < θ < \frac{5 π}{3}$
$\Rightarrow 2 cos θ + 1 \in (1, 2)$
$∴ 1 < 2 sin (θ + ϕ) < 2$
$\Rightarrow \frac{1}{2} < sin (θ + ϕ) < 1 ... (i i i)$
$\Rightarrow \frac{π}{6} < θ + ϕ < \frac{5 π}{6}$
or $\frac{13 π}{6} < θ + ϕ < \frac{17 π}{6}$
$∴ \frac{π}{6} - θ < ϕ < \frac{5 π}{6} - θ$
or $\frac{13 π}{6} - θ < ϕ < (\frac{17 π}{6}) - θ$
$\Rightarrow ϕ \in (- \frac{3 π}{2}, - \frac{2 π}{3}) or (\frac{2 π}{3}, \frac{7 π}{6}), as θ \in (\frac{3 π}{2}, \frac{5 π}{3})$

|

Updated on:21/07/2023

Class 12 MATHS TRIGONOMETRICAL EQUATIONS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Let $θ, ϕ \in [0, 2 π]$ be such that $2 cos θ (1 - sin ϕ) = {sin}^{2} ϕ, (tan \frac{θ}{2} + cot \frac{θ}{2}) cos ϕ - 1, tan (2 π - θ > 0$ and $- 1 < sin θ < - \frac{\sqrt{3}}{2} . T h e n,$ phi cannot satisfy
A $0 < ϕ < \frac{π}{2}$
B $\frac{π}{2} < ϕ < \frac{4 π}{3}$
C $\frac{4 π}{3} < ϕ < \frac{3 π}{2}$
D $\frac{3 π}{2} < ϕ < 2 π$
Question 2 - Select One or More
Let $θ, ϕ \in [0, 2 π]$ be such that $2 cos θ (1 - sin ϕ) = {sin}^{2} θ (tan \frac{θ}{2} + cot \frac{θ}{2}) cos ϕ - 1, tan (2 π - θ) > 0$ and $- 1 < sin θ < \frac{\sqrt{3}}{2}$ , then $ϕ$ cannot satisfy
A $0 < ϕ < \frac{π}{2}$
B $\frac{π}{2} < ϕ < \frac{4 π}{3}$
C $\frac{4 π}{3} < ϕ < \frac{3 π}{2}$
D $\frac{3 π}{2} < ϕ < 2 π$
Question 3 - Select One
If $cos θ + cos ϕ = a$ and $sin θ - sin ϕ = b$ , then: $2 cos (θ + ϕ)$ =
A $a^{2} - b^{2} - 2$
B $a^{2} - b^{2} + 2$
C $a^{2} + b^{2} = 2$
D $a^{2} + b^{2} - 2$

IIT JEE PREVIOUS YEAR-TRIGONOMETRICAL EQUATIONS-OBJECTIVE QUESTIONS II ( ONE OR MORE THAN ONE CORRECT OPTION)

Home
Ask Doubt
Profile