Consider a square OABC ,If P and Q are the midpoints of sides AB and BC ,respectively. Then the value of 2(AreaofΔOPQ)Areaof□OABC is
Step by step video & image solution for Consider a square OABC ,If P and Q are the midpoints of sides AB and BC ,respectively. Then the value of (2(Area of Delta OPQ))/(Area of square OABC) is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
ABCD is a square of area 1 m2. P and Q are the midpoints of AB and BC respectively. What is the area of Δ DPQ ?
View SolutionIn a ΔABCPandQ are the mid-point or AB and AC, respectively. If O is the circume- centre of the ΔABC, then the value of (Area ofΔABCArea of ΔOPQ)cotBcotC equal to
View Solution
Knowledge Check
- Question 1 - Select One
If D, E and F are the mid-points of sides BC, CA and AB respectively of △ABC, then the ratio of the areas of △DEF to the area of △ABC is :
A1:4B1:2C1:3D2:3 - Question 2 - Select One
In the figure, ABCD is a square. E and Fare midpoints of AD and BC respectively. The ratio of areas of ΔGAB and ΔHAB
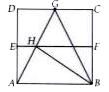 A4 : 1B1 : 4C1 : 2D2 : 1
A4 : 1B1 : 4C1 : 2D2 : 1 - Question 3 - Select One
OPQR is a square with M and N as the middle points of the sides PQ and QR, respectively. The ratio of the areas of the square and the triangle OMN is
A4:1B2:1C8:3D4:3
If D,E and F are the midpoints of sides BC, CA, and Ab respectively of △ABC then using coordinate geometry prove that Area of △DEF= 14 (Area of △ABC)
View SolutionΔABC is an equilateral triangle and D and E are midpoints of AB and BC respectively. Then the area of ΔABC : the area of the trapezium ADEC is
View SolutionABCD is a square inscribed in a circle of radius 14 cm, E,F,G and H are the midpoints of the sides DA, AB, BC and CD respectively. The area of the square EFGH will be
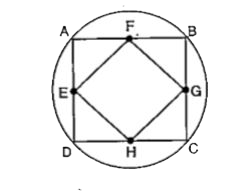 View Solution
View SolutionLet WXYZ be a square. Let P, Q, R, be the midpoints of WX, XY and ZW respectively and K, L be the midpoints of PQ and PR respectively. What is the value of
Area of triangle PKLArea of square WXYZ=?View SolutionOPQR is a square with M and N as the middle points of the sides PQ and QR, respectively. The ratio of the areas of the square and the triangle OMN is
View Solution
