For a set A, consider the following statements:
1.A∪P(A)=P(A) 2.{A}∩P(A)=A
3. P(A)−{A}=P(A)
where P denotes power set.
Which of the statements given above is/are correct?
1 only
2 only
3 only
1, 2 and 3
The correct Answer is:A
Since, Power set is the collection of all the subsets of the set A therefore
A UP (A) = P(A)
∴ statement (1) is correct.
Topper's Solved these Questions
Similar Questions
Write the power set p(x) of the set X={3,4}
View SolutionIf An=Pn+1, where Pn is the product of the first n prime numbers, then consider the following statements :
1. An is always a composite number.
2. An + 2 is always an odd number.
3. An+1 is always an even number.
Which of the above statements is/are correct ?
View Solution
Knowledge Check
If A=P({1, 2}) where P denotes the power set, then which one of the following is correct?
A{1,2}⊂AB1∈AC phi cancel (in) AD{1,2}∈AIf A=P({1, 2}) where P denotes the power set, then which one of the following is correct?
A{1,2}⊂AB1∈ACphi cancelinAD{1,2}∈AIf A =P[1, 2], where P denotes the power set, then which one of the following is correct?
A{1,2}⊂AB1∈ACϕ∈AD{1,2}∈A
A, B are two events and ¯¯¯A denotes the complements of A. Consider the following statements
1. P(A∪B)≤P(B)+P(A)
2. P(A)+P(¯¯¯A∪B)≤1+P(B)
Which of the above statements is/are correct ?
View SolutionConsider the following statements:
1.P(¯¯¯A∪B)=P(¯¯¯A)+P(B)−P(¯¯¯A∩B)
2.P(A∩¯¯¯B)=P(B)−P(A∩B)
3.P(A∩B)=P(B)P(A∣B)
Which of the above statements are correts ?
View SolutionIf A and B are two events that P(A)=34andP(B)=58, then consider the following statements:
1. The minimum value of P(A∪B) is 34.
2. The maximum value of P(A∩B) is 58.
Which of the above statements is/are correct?
View Solution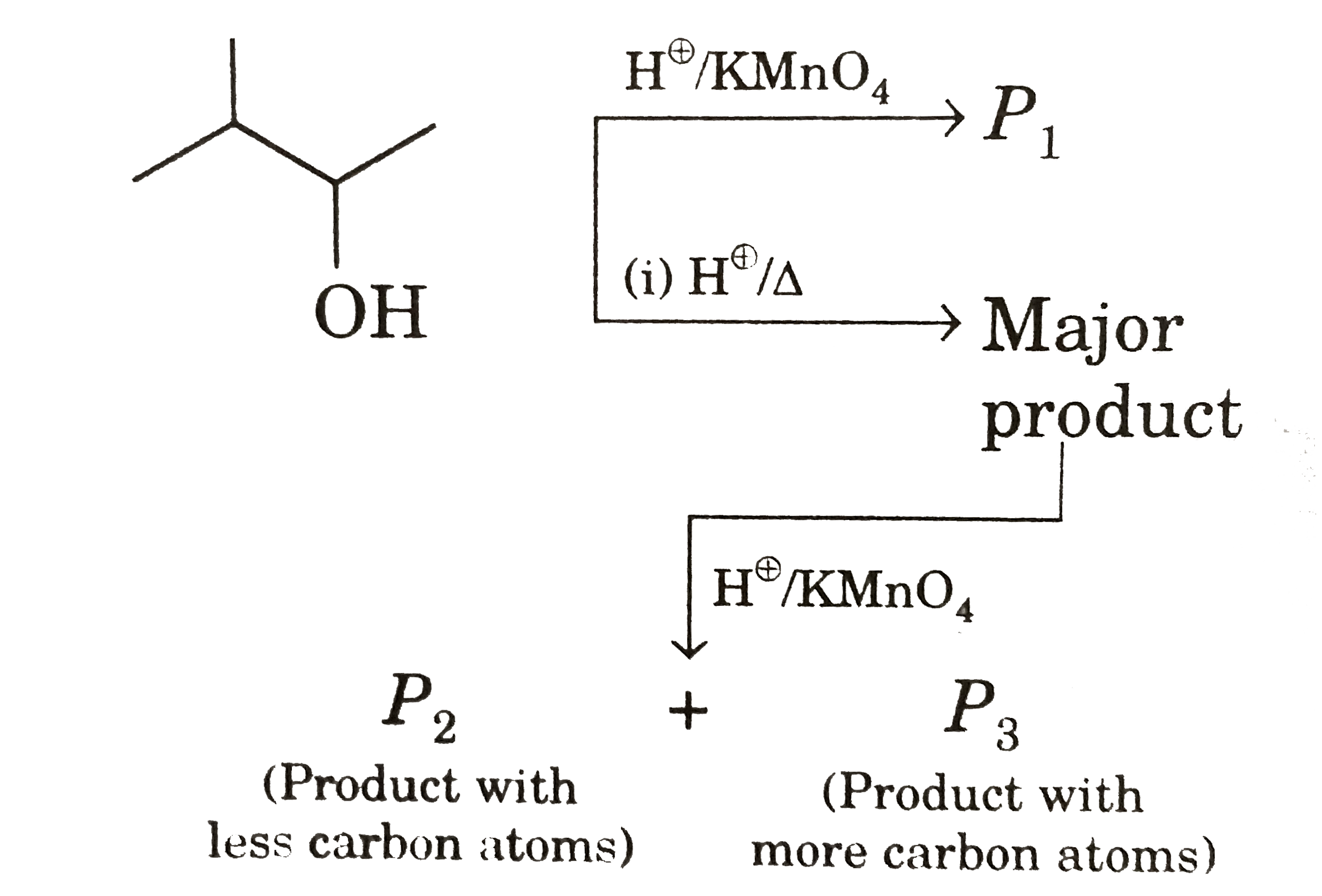
Which of the following statement is not correct about P2 ?
View SolutionThe probability distribution of random variable X with two missing probabilities p1 and p2 is given below
XP(X)1k2p134k4p252k
It is further given that P(X≤2)=0.25andP(X≥4)=0.35. Consider the following statements
1. p1=p2
2. p1+p2=P(X=3)
which of the statements given above is/are correct ?
View Solution
