If A=P({1, 2}) where P denotes the power set, then which one of the following is correct?
{1,2}⊂A
1∈A
phi cancelinA
{1,2}∈A
The correct Answer is:D
To solve the problem, we need to determine the power set of the set {1,2} and analyze the options given in the question.
1. Understanding the Power Set:
The power set P(S) of a set S is the set of all possible subsets of S. For a set with n elements, the power set will have 2n elements.
2. Identify the Set:
Here, we have the set S={1,2}. The number of elements n in this set is 2.
3. Calculate the Number of Subsets:
Since n=2, the number of subsets is 22=4.
4. List All Subsets:
The subsets of {1,2} are:
- The empty set: ∅
- The subset containing only 1: {1}
- The subset containing only 2: {2}
- The subset containing both elements: {1,2}
5. Form the Power Set:
Therefore, the power set A=P({1,2}) is:
A={∅,{1},{2},{1,2}}
6. Analyze the Options:
Now we need to determine which of the following statements is correct:
- {1,2} belongs to A
- ∅ belongs to A
- {1,2} is a subset of A
- 1 belongs to A
From our power set A:
- {1,2} is indeed an element of A.
- The empty set ∅ is also an element of A.
- {1,2} is not a subset of A since it is an element, not a subset.
- The element 1 is not an element of A since A contains sets, not individual elements.
7. Conclusion:
The correct statement is that {1,2} belongs to A.
Final Answer:
The correct option is: {1,2} belongs to A.
The power set P(S) of a set S is the set of all possible subsets of S. For a set with n elements, the power set will have 2n elements.
Here, we have the set S={1,2}. The number of elements n in this set is 2.
Since n=2, the number of subsets is 22=4.
The subsets of {1,2} are:
- The empty set: ∅
- The subset containing only 1: {1}
- The subset containing only 2: {2}
- The subset containing both elements: {1,2}
Therefore, the power set A=P({1,2}) is:
A={∅,{1},{2},{1,2}}
Now we need to determine which of the following statements is correct:
- {1,2} belongs to A
- ∅ belongs to A
- {1,2} is a subset of A
- 1 belongs to A
- {1,2} is indeed an element of A.
- The empty set ∅ is also an element of A.
- {1,2} is not a subset of A since it is an element, not a subset.
- The element 1 is not an element of A since A contains sets, not individual elements.
The correct statement is that {1,2} belongs to A.
The correct option is: {1,2} belongs to A.
Topper's Solved these Questions
Similar Questions
Knowledge Check
Which one of the following is a correct set?
AH2O,sp3 angularBBCl3,sp3, angularCNH+4,dsp2, square planarDCH4,dsp2, tetrahedralIf A=P({1, 2}) where P denotes the power set, then which one of the following is correct?
A{1,2}⊂AB1∈AC phi cancel (in) AD{1,2}∈AWhich one of the following is correct set of SiO2
ALinear, acidicBLinear, BasicCTetrahedral, AcidicDAngular, Basic
If A is any set and P(A) is its power set, then which of the following is/are correct? 1. P(A)∩P(B)=P(A∩B) II. P(A)∪P(B)=P(A∪B) Select the correct answer using the code given below.
View SolutionV vs T curves at different pressures P1 and P2 for an ideal gas are shown below:
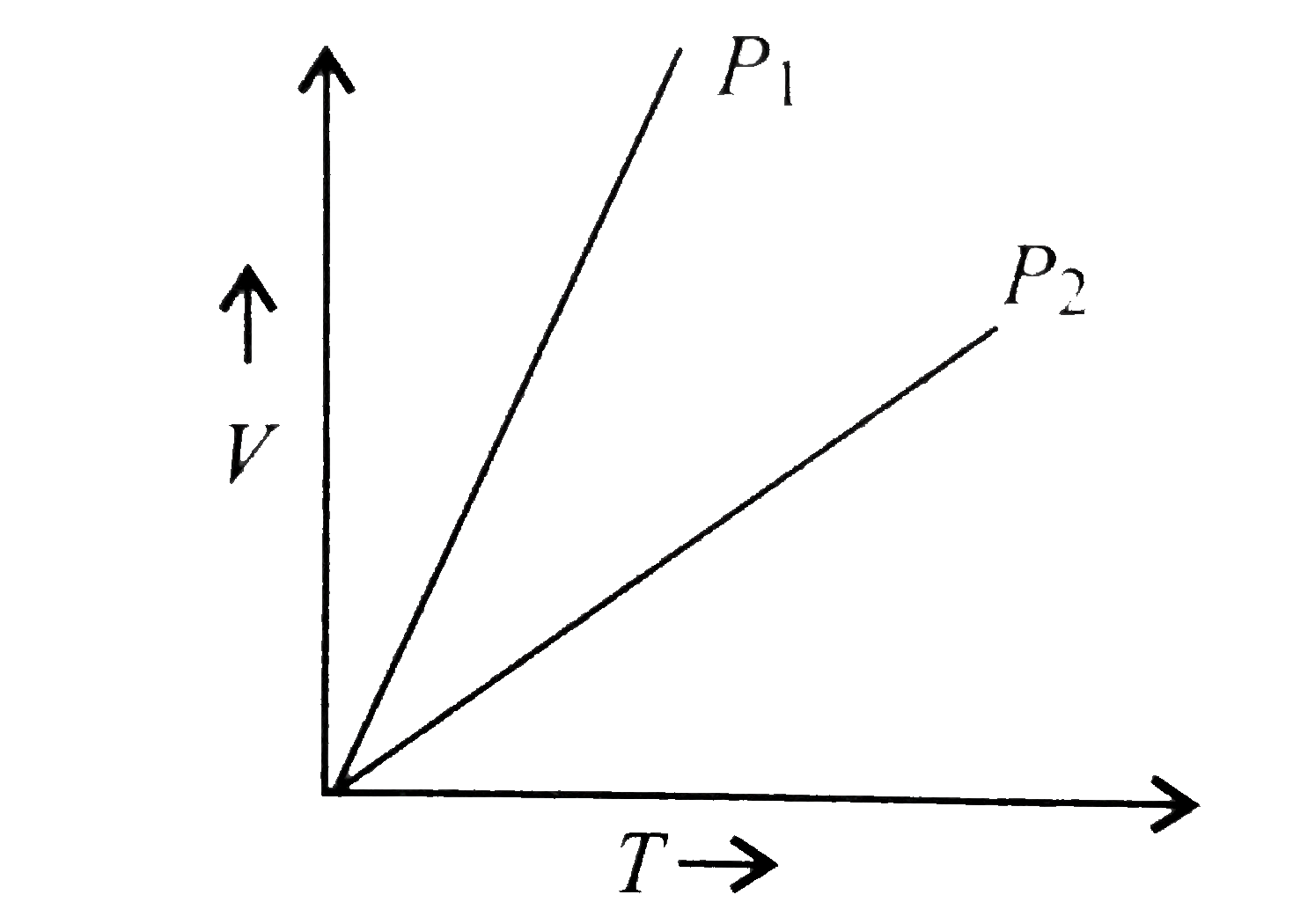
Which one of the following is correct?
View SolutionLet A and B be two sets, and P(A) denotes the power set of A, then which of the following is true?
View SolutionIf A and B are events such that P(A∣B)=P(B∣A), then
View SolutionIf E is the electric field in uniform conductor, l is the current and Va and P denotes drift velocity and thermal power produced, then which of the following is correct:
View Solution