In what ratio do the coordinate axes divide the line segment joining (-2,5) and (3,-4) .
8x+5y+20=0
5x+8y−7=0
8x−5y+60=0
5x−8y+57=0
The correct Answer is:C
Let A(a, 0) and B(0, b) be two points on x-axis and y-axis respectively
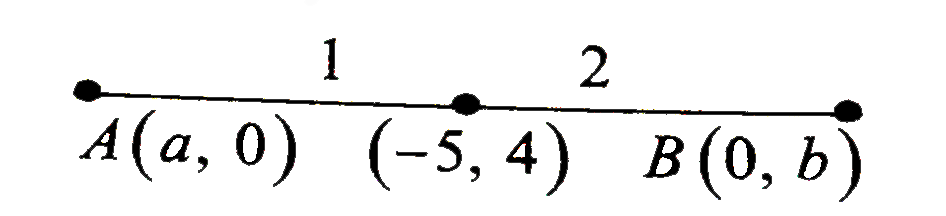
Given (-5, 4) divides line AB in the ratio 1 : 2. By section formula we have
−5=1×0+2×a3
⇒a=−152 and 4=1×b+2×03
⇒b=12
Thus, A=(=152,0) and B=(0,12)
Hence, equation of line joining (−152,0) and (0,12) is
(y−0)=12−00+152.(x+152)
⇒y=45(2x+15)
⇒5y=(8x+60)⇒8x−5y+60=0
Topper's Solved these Questions
Similar Questions
Knowledge Check
Find the coordinate of the point which divides the line segment joining A(1,−2,3)andB(3,4,−5) in the ratio 2:3 externally.
A(3,14,19)B(−3,−14,19)C(−3,14,19)DNone of these
In what ratio does the x=axis divide the line segment joining the points (2,−3) and (5, 6)?
View Solutiony -axis divides the line segment joining (1,4) and (−3,5) in the ratio
View SolutionIn what ratio does the X -axis divide the line segment joining the points (-4,-6) and (-1,7) ? Find the coordinates of the points of division.
View Solution(ii)In what ratio does the x axis divide the line segment joining the points (2;−3)and(5;6). Find the coordinate of a point of intersection
View SolutionIn what ratio does y-axis divide the line segment joining the points (-4, 7) and (3, -7)?
View SolutionIn what ratio does the point (3,−2) divide the line segment joining the points (1,4) and (−3,16)
View SolutionFind the coordinates of the point which divides the line segment joining (−1, 3) and (4, −7) internally in the ratio 3:4 .
View Solution
