The locus of a point which is equidistant from the x−axis and the y−axis is
A
y=2x
B
x=2y
C
y=±x
D
2y+x=0
Video Solution
Text Solution
The correct Answer is:C
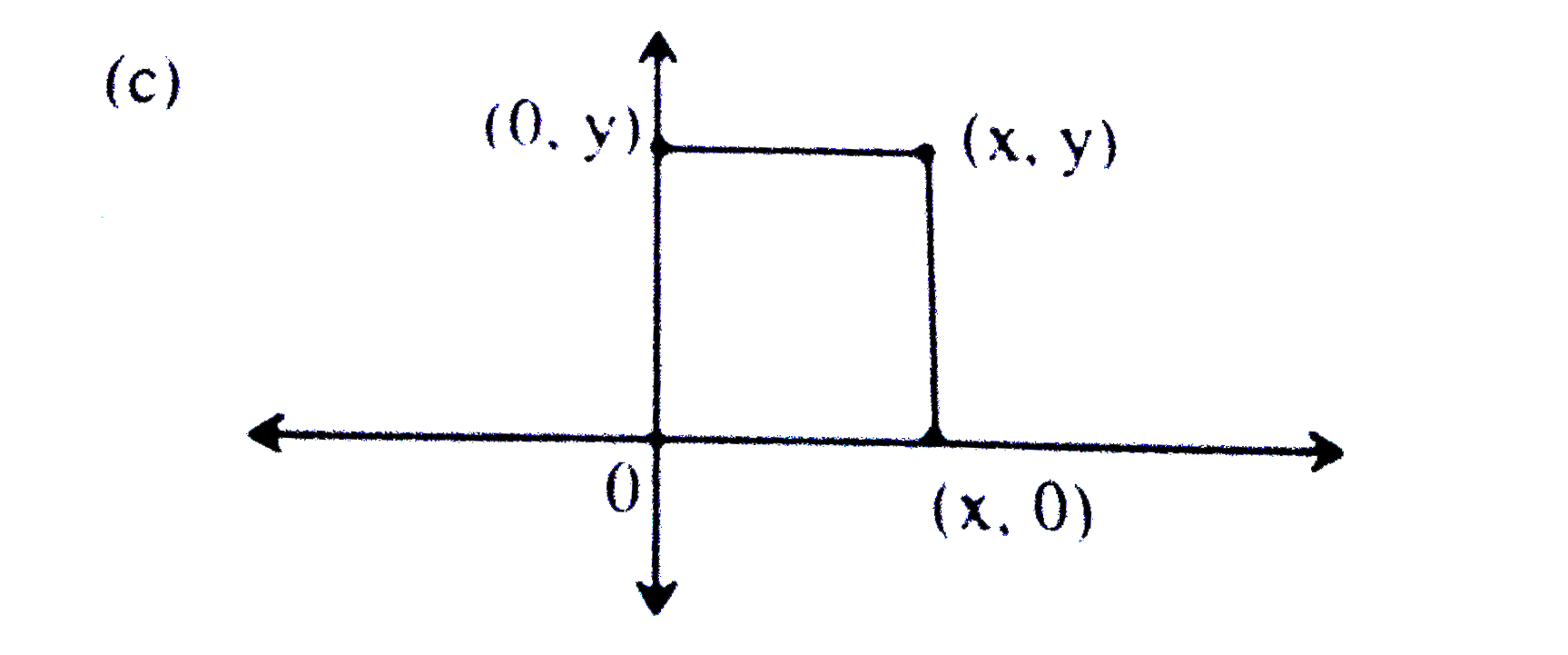
√(x−0)2+(y+y)2=√(x−x)2+(y−0)2
⇒√(x−0)2=√(y−0)2
⇒√x2=√y2
⇒y=±x
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
The locus of a point which is equidistant from point (4,2) and x-axis is
Ah2−8h−4k+20=0Bh2−8h+4k−20=0Ch2−6h+4k+20=0DNone of theseThe locus of a point which is equidistant from point (4,2) and x-axis is
Ah2−8h−4k+20=0Bh2−8h+4k−20=0Ch2−6h+4k+20=0DNone of theseLocus of all such points which is equidistant from (1, 2) and x-axis is
Ax2−2x−4y+5=0Bx2+2x−4y+5=0Cx2−2x+4y+5=0DNone of these
The equation to the locus of the point P(x,y) which is equidistant from the coordinate axes is
View SolutionFind the locus of a point equidistant from the point (2,4) and the y-axis.
View SolutionIf the locus of the point which is equidistant from (2,0) to the Y -axis is y2=a(x−1) ,then the value of a2+4 is equal to
View SolutionIf the locus of the point which is equidistant from (2,0) to the Y-axis is y2=a(x−1) ,then the value of a2+4 is equal to
View Solution(1)The equation of locus of the point whose the distance from the x-axis is twice that of from the y-axis is (2)The equation of the locus of the point which moves equidistant form the coordinate axes is
View Solution
