Find the area enclosed by the parabola 4y=3x2 and the line 2y=3x+12.
A
27 square unit
B
36 squre unit
C
48 square unit
D
54 square unit
Video Solution
Text Solution
The correct Answer is:A
Equation of line 2y=3x+12,y=3x+122
Equation of parabola 4y=3x2,y=3x24
∫4−2[3x+122−3x24]dx
=12[3x22+12x]4−2−34[x33]4−2
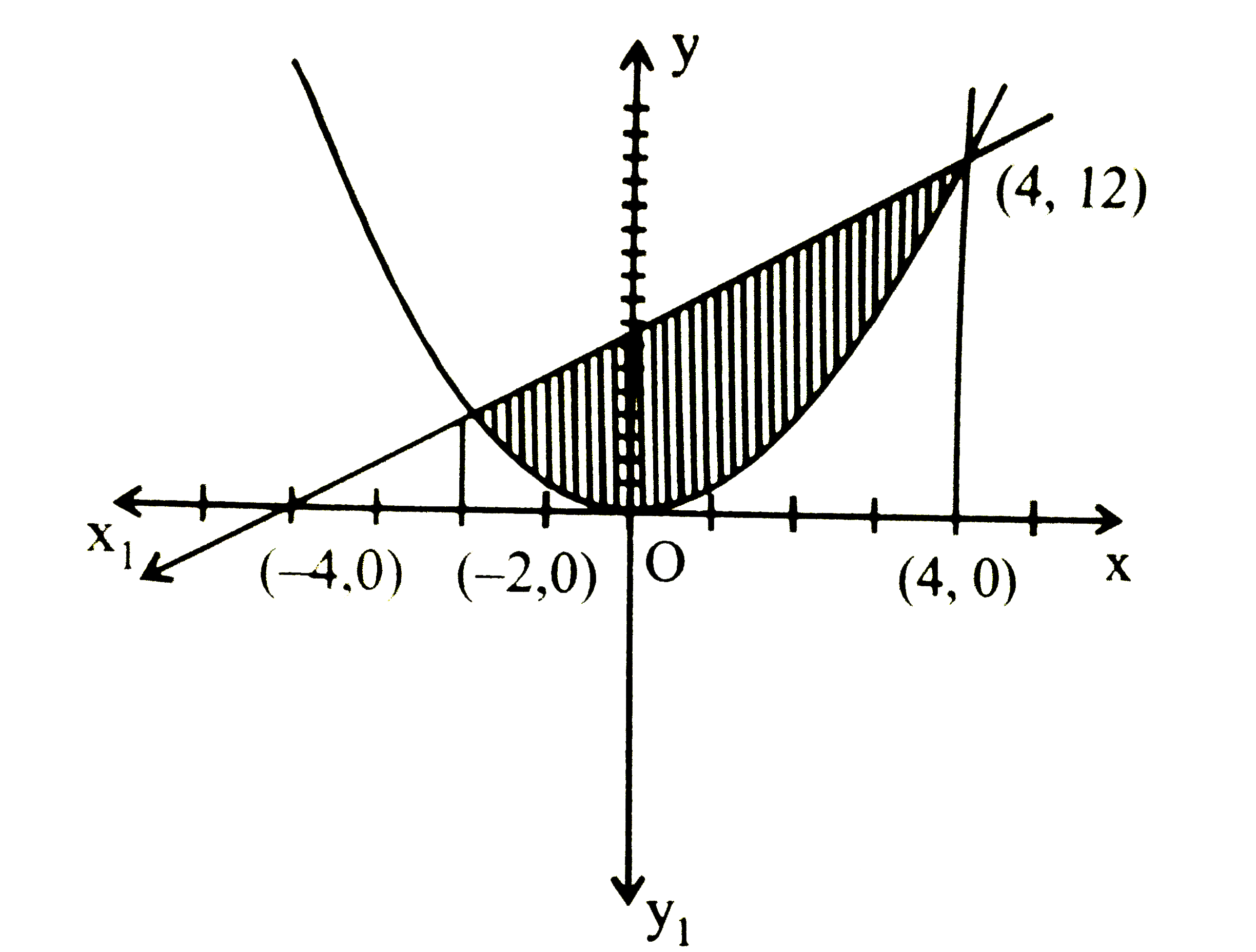
=12[{3(4)22+12(4)}−{3(−2)22+12(−2)}]−34[433−(−2)33]
=12[24+48−6+24]−34[64+83]
12×90−18=27sq. units.
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
The area enclosed by the parabola y=3(1−x2) and the x-axis is
A4B3C9D2The area bounded by the parabola x2=2y and the line y=3x is
A4 sq. unitsB18 sq. unitsC24 sq. unitsD32 sq. unitsIf the area enclosed between the parabola y2=4x and the line y = mx is (1/3) sq. unit, then : m =
A1B2C3D4
Find the area of the region enclosed by the parabola x2=y and the line y = x+ 2.
View SolutionFind the area of the region enclosed by the parabola x2=y and the line y = x+ 2.
View SolutionFind the area cut off from the parabola 2y=3x2 by the line 2y=3x+12.
View SolutionFind the area enclosed by the parabola y=2−x2 and the straight line x + y = 0
View SolutionThe area enclosed between the parabola y=x2−x+2 and the line y = x + 2 (in sq unit) equals to
View Solution