The point on y2=4ax nearst to the focus has to abscissa equal to
x=0
x=a
x=a2
x=2a
The correct Answer is:A
Here, 'S' represents focus O(0, 0) is a on parabola y2=4ax and nearest to focus (a, 0)
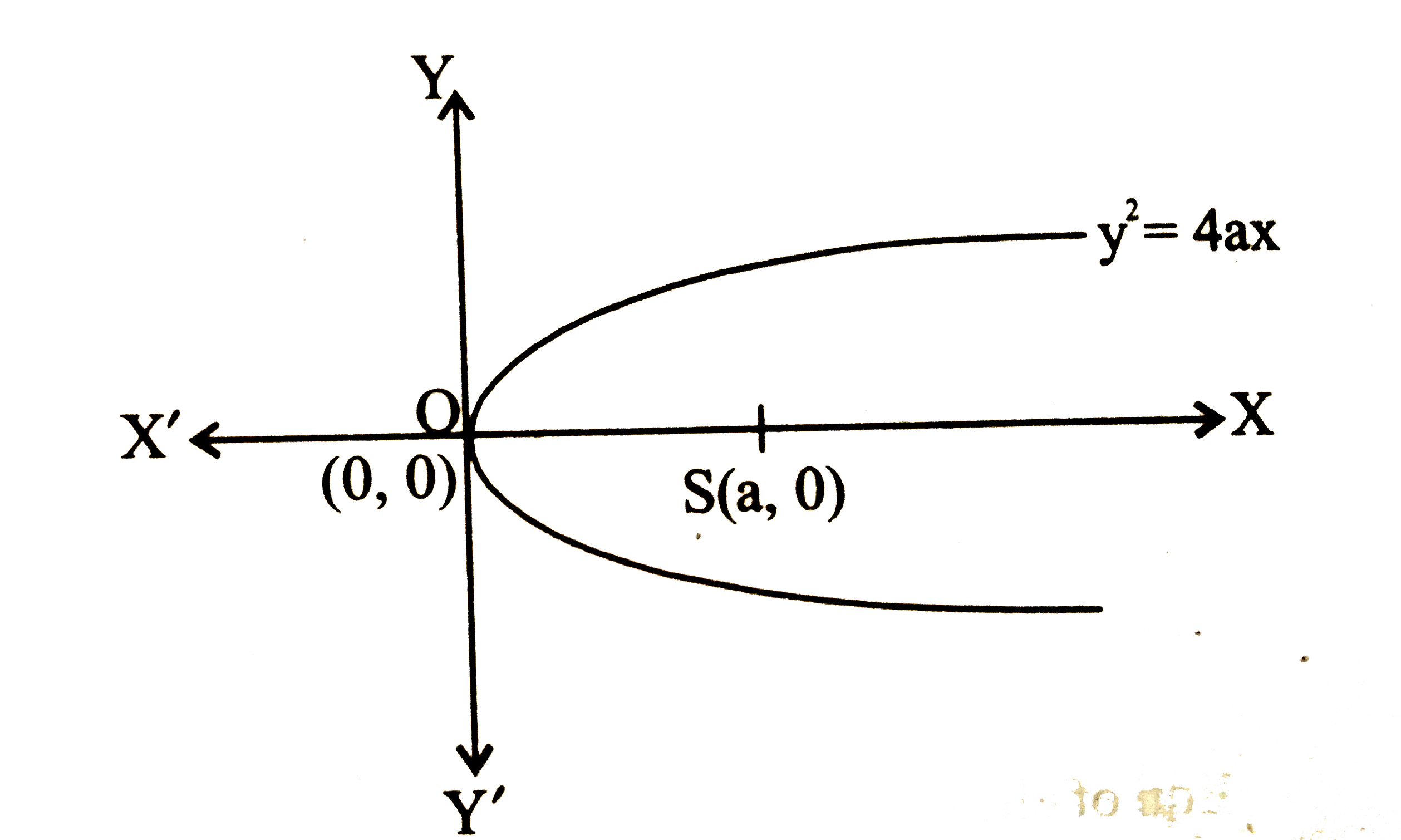
∴ abscissa of O(0, 0) is x = 0
∴ Option (a) is correct.
Topper's Solved these Questions
Similar Questions
Knowledge Check
The point on y2=4ax nearest to the focus has to abscissa equal to
A−aBaCa/2D0The point on the parabola y2=4ax nearest to the focus has its abscissa.
Ax=0Bx=aCx=a2Dx=2a
In the parabola y2=4ax, the tangent at the point P, whose abscissa is equal to the latus ractum meets the axis in T & the normal at P cuts the parabola again in Q. Prove that PT : PQ = 4 : 5.
View SolutionThe point on the curve y2=4ax at which the normal makes equal intercepts on the coordinate axes is
View SolutionIn the parabola y2=4ax, then tangent at P whose abscissa is equal to the latus rectum meets its axis at T, and normal P cuts the curve again at Q. Show that PT:PQ=4:5.
View SolutionIf "P" is a point on the parabola "y2=4ax" in which the abscissa is equal to ordinate then the equation of the normal at "P" is
View SolutionThe normal meet the parabola y2=4ax at that point where the abscissa of the point is equal to the ordinate of the point is
View SolutionFor the parabola y2=4ax, the ratio of the subtangent to the abscissa, is
View Solution
