There are n-points (n>2) in each to two parallel lines. Every point on one line is joined to every point on the other line by a line segment drawn within the lines. The number of point (between the lines) in which these segments intersect, is
2nC2−2.nC1+2
2nC2−2×nC2
nC2×nC2
none of these
The correct Answer is:C
Step by step video, text & image solution for There are n-points (ngt2) in each to two parallel lines. Every point on one line is joined to every point on the other line by a line segment drawn within the lines. The number of point (between the lines) in which these segments intersect, is by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
Every point on a number line represents.
Aa rational numberBa natural numberCan irrational numberDa unique real number25 lines are drawn in a plane such that no two of them are parallel and no three of them are concurent. The number of points in which these lines intersect, is
A300B315C325D45025 lines are drawn in a plane. Such that no two of them are parallel and no three of them are concurrent. The number of points in which these lines intersect, is:
A300B315C325D450
Two line segments may intersect at two points
View SolutionIf the mid-point of the line segment between the axes of a line is (p,q) then find the equation of the line.
View SolutionThe point C is the image of point A in line l and line segment BC intersects the line l at P.
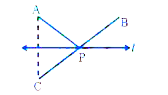
Is the image of P in line l the point P itself ?
View Solution15 lines are drawn in a plane in such a way that no two of them are parallel and no three are concurrent. The number of points of intersections of these lines is
View SolutionA (-1, 4) and B(5, 4) are the end points of a line segment, find the coordinates of the mid points of the line segment :
View Solution
