ifC0C1C2,……Cn are the binomial coefficients in the expansion of (1+x)n then prove that:
C0C2+C1C3+C2C4+……+Cn−2Cn=∣2–n|n––−2|n––+2
(2n)!(n−2)!(n+2)!
(2n)!((n−2)!)2
(2n)!((n+2)!)2
none of these
The correct Answer is:A
Step by step video, text & image solution for " if" C_(0)C_(1)C_(2),……C_(n) are the binomial coefficients in the expansion of (1+x)^(n) then prove that: C_(0)C_(2)+C_(1)C_(3)+C_(2)C_(4)+……+C_(n-2)C_(n)=(|ul2n)/(|uln-2|uln+2) by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - OBJECTIVE RD SHARMACHAPTER - BINOMIAL THEOREM AND ITS APPLCIATIONS EXERCISE - Chapter Test60videos
BINOMIAL THEOREM AND ITS APPLCIATIONS
- BOOK - OBJECTIVE RD SHARMACHAPTER - BINOMIAL THEOREM AND ITS APPLCIATIONS EXERCISE - Section I - Assertion Reason Type13videos
BINOMIAL THEOREM AND ITS APPLCIATIONS
- BOOK - OBJECTIVE RD SHARMACHAPTER - CARTESIAN CO-ORDINATE SYSTEM EXERCISE - Exercise29videos
CARTESIAN CO-ORDINATE SYSTEM
Similar Questions
Knowledge Check
- Question 1 - Select One
If C0,C1,C2,…,Cn denote the binomial coefficients
in the expansion of (1+x)n, then
C02+2C12+3C22+...+(n+1)Cn2=A(2n+1)2nCnB(2n−1)2nCnC(n2+1)2nCnD(n2+1)2n−1Cn - Question 2 - Select One
If C0,C1,C2,…,Cn denote the binomial
coefficients in the expansion of (1+x)n, then n∑r=0n∑s=0(Cr+Cs)A(n+1)2B(n+1)2n+1Cn2nDn2n+1 - Question 3 - Select One
If C0,C1,C2,…,Cn denote the binomial
coefficients in the expansion of (1+x)n , then n∑r=0n∑s=0CrCs=A2nBn2nC22nD2nCn
In C0,C1C2….Cn are the binomial coefficients in the expansion of (1+x)n then prove that :
(i)C20−C21+C22−C23+…..+(−1)n.C2n
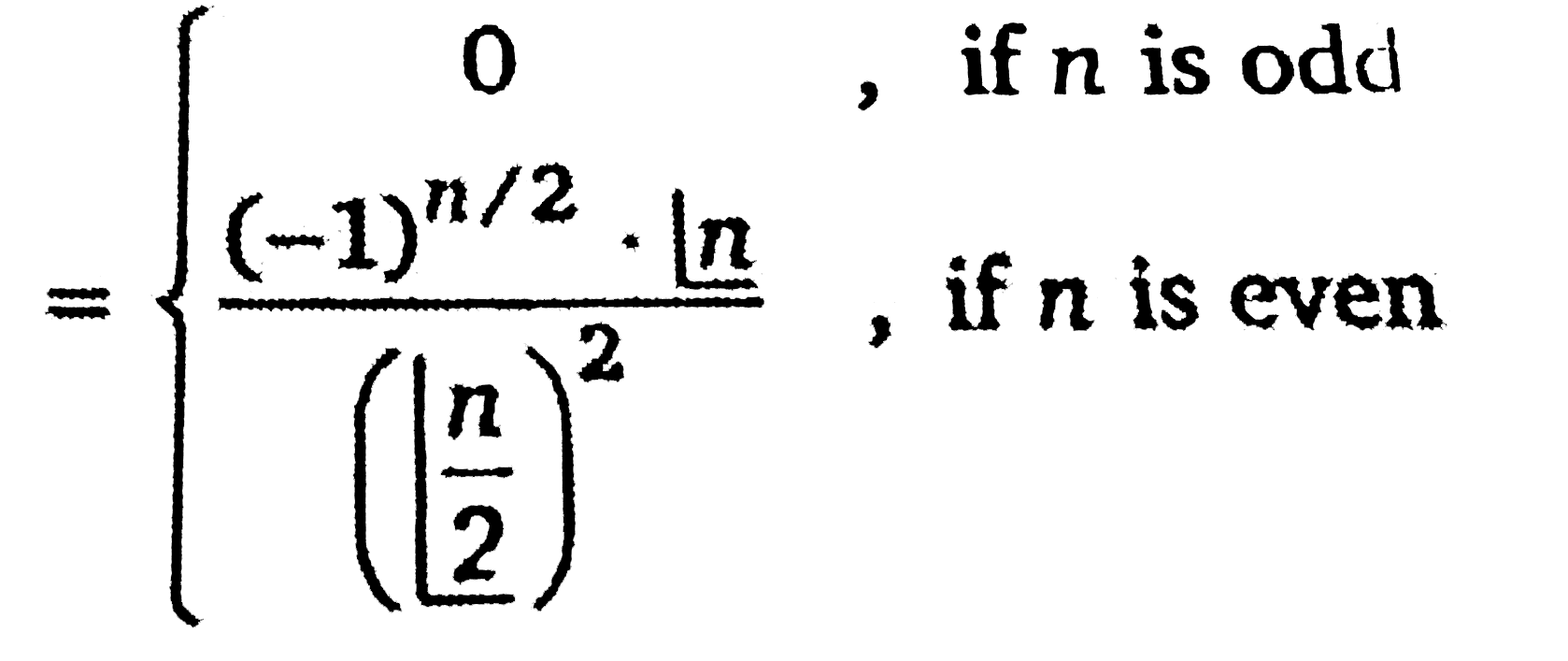
(ii)C0C1+C1C2+C2C3+....+Cn−1Cn
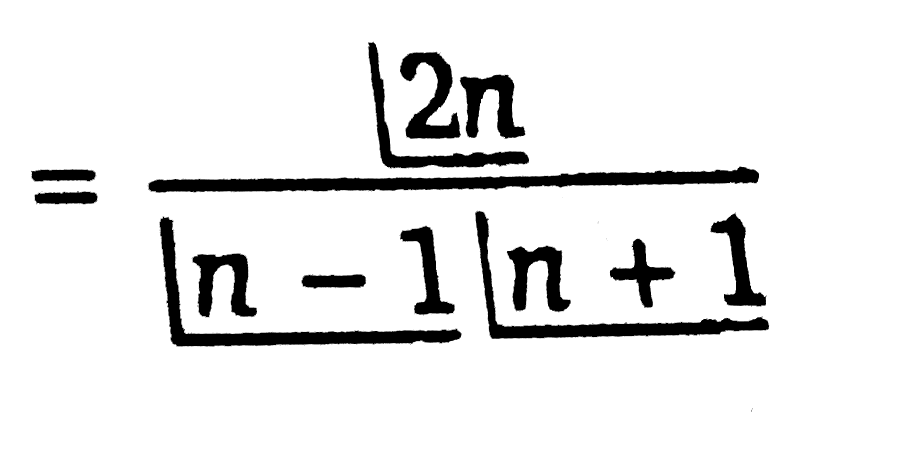 View Solution
View SolutionIf C0,C1,C2,…,Cn are the binomial coefficients
in the expansion of (1+x)n , prove that
(C0+2C1+C2)(C1+2C2+C3)…(Cn−1+2Cn+Cn+1)
(n−2)n(n+1)!n∏r=1(Cr−1+Cr).View SolutionIf CoC1,C2,.......,Cn denote the binomial coefficients in the expansion of (1+x)n, then the value of n∑r=0(r+1)Cr is
View SolutionIf C0,C1,C2,.......,Cn denote the binomial coefficients in the expansion of (1+1)n, then ∑0≤r∑<s≤n(Cr+Cs)
View SolutionIf C0,C1,C2,…,Cn are the coefficients in the expansion of (1+x)n, then what is the value of C1+C2+C3+….+Cn ?
View Solution

