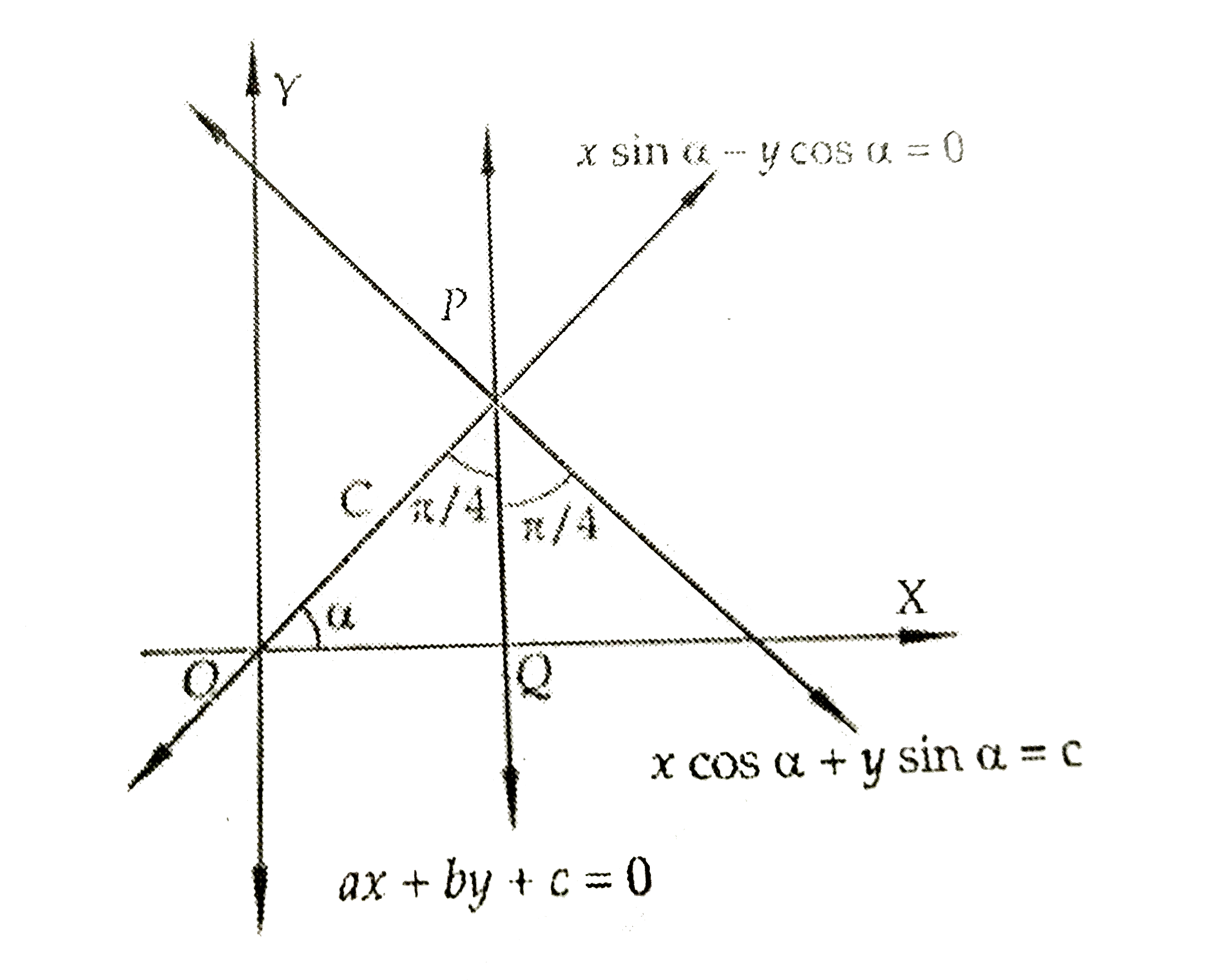
If the straight lines $a x + b y + c = 0$ and $x cos α + y sin α = c$ encloses an angle of $\frac{π}{4}$ between them and meet the straight line $x sin α - y cos α = 0$ in the point then

$a^{2} + b^{2} = c^{2}$

$a^{2} + b^{2} = 2 c^{2}$

$a^{2} + b^{2} = 4$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Updated on:21/07/2023

If the straight lines $a x + b y + p = 0$ and $x cos α + y sin α - p = 0$ enclose an angle $π / 4$ between them and meet the straight line $x sin α - y cos α = 0$ in the same point, then the value of $a^{2} + b^{2}$ is equal to ………..
A ${sin}^{2} α = 1$
B ${cos}^{2} α = 1$
C ${sin}^{2} α = a^{2}$
D ${cos}^{2} α = a^{2}$
The four lines $a x + b y + c = 0$ enclose a
Asquare
Bparallelogram
Crectangle
Drhombus whose are is $\frac{2 c^{2}}{a b}$
The line $a x + b y + c = 0$ intersects the line $x cos α + y sin α = c$ at the point P and angle between them is $π / 4$ . If theline $x sin α - y cos α$ also passes through the point P, then
A $a^{2} + b^{2} = c^{2}$
B $a^{2} + b^{2} = 2 c^{2}$
C $a^{2} + b^{2} = 2$
D $a^{2} + b^{2} = 4$