Let ABC be an isosceles triangle with AB=BC. If base BC is parallel to x-axis and m1andm2 are the slopes of medians drawn through the angular points BandC, then
m1,m2=2
m1+m2=0
m1m2=2
m1+2m2=0
The correct Answer is:B
Step by step video, text & image solution for Let ABC be an isosceles triangle with AB = BC. If base BC is parallel to x-axis and m_1 and m_2 are the slopes of medians drawn through the angular points B and C, then by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
△ABC is an isosceles triangle with AB=AC=15cm and altitude from A to BC is 12 cm. The length of sides BC is :
A9 cmB12 cmC18 cmD20 cm - Question 2 - Select One
In an isosceles triangle ABC,AB=AC,XY∣∣BC. If ∠A=30∘, then ∠BXY=?
A75∘B30∘C150∘D105∘ - Question 3 - Select One
ΔABC is an isosceles triangles with AB = AC = 10 cm,AD =8 cm M is the median on BC from A. The length of BC is
A8 cmB12 cmC10 cmD6 cm
ABC is an isosceles triangle with AC=BC . If AB2=2 AC2 , prove that ABC is right triangle.
View SolutionIn the figure, ABC is an isosceles triangle in which AB = AC and LM is parallel to BC. If ∠A=50∘ find ∠LMC.
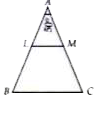 View Solution
View SolutionABC is an isosceles triangle with AB=AC and D is a point on AC such that BC2=ACxCD. Prove that BD=BC
View SolutionIn a triangle ABC, AB is parallel to y-axis, BC is parallel to x-axis, centroid is at (2, 1), If median through C is x−y=1, then the slope of median through A is
View SolutionABC is an isosceles triangle in which AB = AC. Prove that the tangent to the circum-circle at A is parallel to BC.
View Solution

