A random variable X has the following probability distribution :
X:12345678P(X):0.150.230.120.100.200.080.070.08
for the events E=[X is a prime number] F={X<4}, the probability P(EOP), is.
0.50
0.77
0.35
0.87
The correct Answer is:B
To solve the problem, we need to find the probability of the union of two events: E (where X is a prime number) and F (where X is less than 4). We will follow these steps:
Step 1: Identify the Prime Numbers
First, we need to identify which values of X are prime numbers. The prime numbers from the set {1, 2, 3, 4, 5, 6, 7, 8} are:
- 2
- 3
- 5
- 7
Step 2: Calculate the Probability of Event E
Next, we calculate the probability of event E, which is the sum of the probabilities of X being a prime number:
- P(X = 2) = 0.23
- P(X = 3) = 0.12
- P(X = 5) = 0.20
- P(X = 7) = 0.07
Now we add these probabilities:
P(E)=P(X=2)+P(X=3)+P(X=5)+P(X=7)
P(E)=0.23+0.12+0.20+0.07=0.62
Step 3: Calculate the Probability of Event F
Now, we calculate the probability of event F, which is the sum of the probabilities of X being less than 4:
- P(X = 1) = 0.15
- P(X = 2) = 0.23
- P(X = 3) = 0.12
Now we add these probabilities:
P(F)=P(X=1)+P(X=2)+P(X=3)
P(F)=0.15+0.23+0.12=0.50
Step 4: Calculate the Intersection of Events E and F
Next, we need to find the intersection of events E and F, which is the probability that X is both a prime number and less than 4. The prime numbers less than 4 are:
- 2
- 3
Now we add the probabilities:
P(E∩F)=P(X=2)+P(X=3)
P(E∩F)=0.23+0.12=0.35
Step 5: Calculate the Probability of E Union F
Finally, we use the formula for the probability of the union of two events:
P(E∪F)=P(E)+P(F)−P(E∩F)
Substituting the values we found:
P(E∪F)=0.62+0.50−0.35
P(E∪F)=0.77
Final Answer
Thus, the probability P(E∪F) is 0.77.
---
First, we need to identify which values of X are prime numbers. The prime numbers from the set {1, 2, 3, 4, 5, 6, 7, 8} are:
- 2
- 3
- 5
- 7
Next, we calculate the probability of event E, which is the sum of the probabilities of X being a prime number:
- P(X = 2) = 0.23
- P(X = 3) = 0.12
- P(X = 5) = 0.20
- P(X = 7) = 0.07
P(E)=P(X=2)+P(X=3)+P(X=5)+P(X=7)
P(E)=0.23+0.12+0.20+0.07=0.62
Now, we calculate the probability of event F, which is the sum of the probabilities of X being less than 4:
- P(X = 1) = 0.15
- P(X = 2) = 0.23
- P(X = 3) = 0.12
P(F)=P(X=1)+P(X=2)+P(X=3)
P(F)=0.15+0.23+0.12=0.50
Next, we need to find the intersection of events E and F, which is the probability that X is both a prime number and less than 4. The prime numbers less than 4 are:
- 2
- 3
P(E∩F)=P(X=2)+P(X=3)
P(E∩F)=0.23+0.12=0.35
Finally, we use the formula for the probability of the union of two events:
P(E∪F)=P(E)+P(F)−P(E∩F)
Substituting the values we found:
P(E∪F)=0.62+0.50−0.35
P(E∪F)=0.77
Thus, the probability P(E∪F) is 0.77.
Topper's Solved these Questions
- DISCRETE PROBABILITY DISTRIBUTIONSBOOK - OBJECTIVE RD SHARMACHAPTER - DISCRETE PROBABILITY DISTRIBUTIONSEXERCISE - Section I - Solved Mcqs
39 Videos
- DISCRETE PROBABILITY DISTRIBUTIONSBOOK - OBJECTIVE RD SHARMACHAPTER - DISCRETE PROBABILITY DISTRIBUTIONSEXERCISE - Section II - Assertion Reason Type
1 Videos
- DETERMINANTSBOOK - OBJECTIVE RD SHARMACHAPTER - DETERMINANTSEXERCISE - Chapter Test
30 Videos
- FUNCTIONSBOOK - OBJECTIVE RD SHARMACHAPTER - FUNCTIONSEXERCISE - Chapter Test
30 Videos
Similar Questions
Knowledge Check
A random variable has the following probability dustribution.
x:01234567p(x):02p2p3pp22p27p22p
The value of p, isA1/10B−1C−1/10Dnone of theseA random varibale X has the following probability distribution.
X:12345P(X):00.10.20.30.4
The mean and standard deviation of X are respectively.A2 and 3B3 and 1C3and√2D2 and 1Select and write the correct answer from the given alternatives in each of the following :
A random variable X has the following probability distribution :
X=x−2−10123P(x)0.10.10.20.20.30.1
Then E(x) = ………A0.8B0.9C0.7D1.1
A random variable X has the following probability distribution: Values of X: −2 −1 0 1 2 3 P(X):0.1 k 0.2 2k 0.3 k
View SolutionA random variable X has the following probability distribution: [X=x0123P(X=x)181214k]
View SolutionA random variable X has the following probability distribution:Determine (i) k (ii) P(X<3)(iii) P(X>6) (iv) P(0<X<3)
View SolutionDetermine which of the following can be probability distributions of a random variable X: X: 0 1 2 3 4 P(X): 0.1 0.5 0.2 −0.1 0.3
View SolutionA random variable X has the following probability distribution:
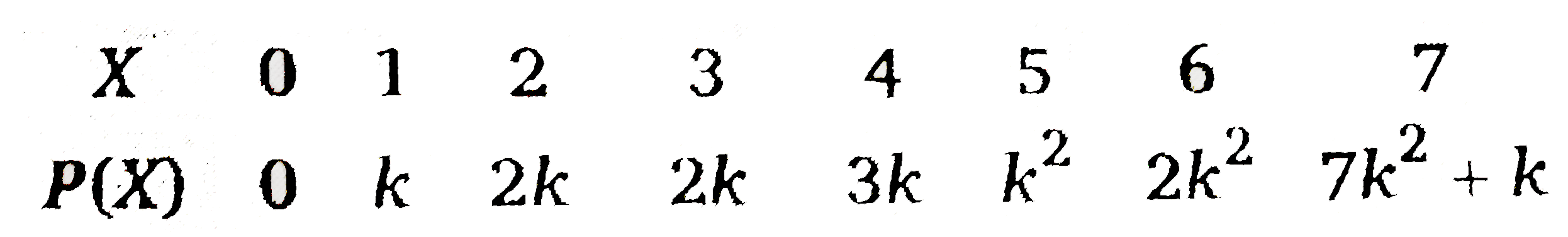
Determine :
(i) k
(ii) P(X<3)
(iii) P(X>6)
(iv) P(0<X<3)
View Solution


