find the value of the
A
±√nπ,n∈{0,1,2,….}
B
±√nπ,n∈{1,2,…}
C
π2+2nπ,n∈{…,−2,−1,0,1,2,…}
D
2nπ,n∈{…−2,−1,0,1,2,…}
Video Solution
Text Solution
The correct Answer is:A
We have, f(x)=x2andg(x)=sinx
∴(fogogof)(x)=(fog)(gof(x))=(fog)(g(f(x)))=(fog)=(sin2)
=f(g(sinx2)=f(sin(sinx2)=sin2(sinx2)
and, (gogof)(x)=(gog)(f(x))=(gog)(x2)=g(g(x2)
∴(fogogof)(x)=(gofog)(x)
⇒sin2(sinx2)=sin(sinx2)
⇒sin(sin2)=sin(sins2)
⇒sin(sinx2){sin(sinx2)−1)}=0
⇒sin(ξnx2)=0or,sin(sinx2)=1
sinx2=nπ,n∈Zor,sinx2=2mπ+π2,m∈Z
⇒sinx2=0
⇒x2=nπ,n∈Z
⇒=±√nπ,n∈{0,1,2,3,......}
|
Topper's Solved these Questions
- REAL FUNCTIONS BOOK - OBJECTIVE RD SHARMACHAPTER - REAL FUNCTIONS EXERCISE - Section II - Assertion Reason Type
8 Videos
- REAL FUNCTIONS BOOK - OBJECTIVE RD SHARMACHAPTER - REAL FUNCTIONS EXERCISE - Exercise
95 Videos
- REAL FUNCTIONS BOOK - OBJECTIVE RD SHARMACHAPTER - REAL FUNCTIONS EXERCISE - Chapter Test
60 Videos
- PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMBOOK - OBJECTIVE RD SHARMACHAPTER - PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMEXERCISE - Chapter Test
55 Videos
- SCALAR AND VECTOR PRODUCTS OF THREE VECTORS BOOK - OBJECTIVE RD SHARMACHAPTER - SCALAR AND VECTOR PRODUCTS OF THREE VECTORS EXERCISE - Exercise
65 Videos
Similar Questions
Knowledge Check
Find the value of X
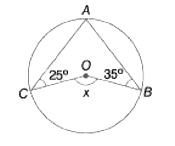 A75∘B120∘C45∘D80∘
A75∘B120∘C45∘D80∘
