Here we find a missing force by using the acceleration. In the overhead view of Fig. 5-4a, a 2.0 kg cookie tin is accelerated at $3.0 m / s^{2}$ in the direction shown by $\to a$ , over a frictionless horizontal surface. The acceleration is caused by three horizontal forces, only two of which are shown: ${\to F}_{1}$ of magnitude 10 N and ${\to F}_{2}$ of magnitude 20 N. What is the third force ${\to F}_{3}$ in unit-vector notation and in magnitude-angle notation?

Text Solution

Verified by Experts

The net force ${\to F}_{net}$ on the tin is the sum of the tree forces and is related to the acceleration $\to a$ via Newton.s second law $({\to F}_{net} = m \to a)$ . Thus,
${\to F}_{1} + {\to F}_{2} + {\to F}_{3} = m \to a, (5 - 6)$
which gives us
${\to F}_{3} = m \to a - {\to F}_{1} - {\to F}_{2} . (5 - 7)$
Calculations: Because this is a two-dimensional problem, we cannot find ${\to F}_{3}$ merely by substituting the magnitudes for the vector quantities on the right side of Eq. 5-7. Instead, we must vectorially add $m \to a, - {\to F}_{1}$ (the reverse of ${\to F}_{1}$ ), and $- {\to F}_{2}$ (the reverse of ${\to F}_{2}$ ), as shown in Fig. 5-4b. This addition can be done directly on a vector-capable calculator because we know both magnitude and angle for all three vectors. However, here we shall evaluate the right side of Eq. 5-7 in terms of components, first along the x axis and then along the y axis. Caution: Use only one axis at a time.

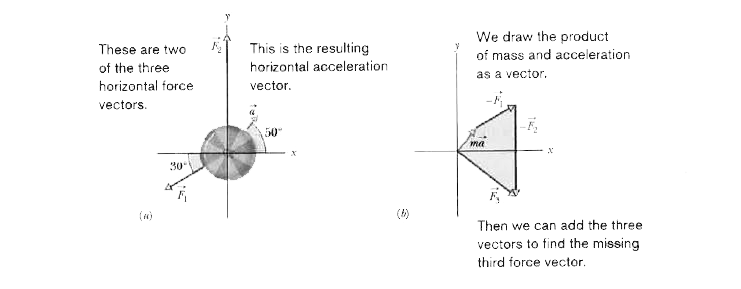
Figure 5-4 (a) An overhead view of two three horizontal forces that act on a cookie tin, resulting in acceleration $\to a . {\to F}_{3}$ is not shown. (b) An arrangement of vectors $m \to a, - {\to F}_{1}$ , and $- {\to F}_{2}$ to find force ${\to F}_{3}$ .
x components: Along the x axis we have
$F_{3, x} = m a_{x} = F_{1, x} - F_{2, x}$
$= m (a {cos 50}^{\circ}) - F_{1} cos (- 150^{\circ}) - F_{2} {cos 90}^{\circ}$ .
Then, substituting known data, we find
$F_{3, x} = (2.0 kg) (3.0 m / s^{2}) {cos 50}^{\circ} - (10 N) cos (- 150^{\circ})$
$- (20 N) {cos 90}^{\circ}$
$= 12.5$ N.
y comonents: Similarly, along the y axis we find
$F_{3, y} = m a_{y} - F_{1, y} - F_{2, y}$
$= m (a {sin 50}^{\circ}) - F_{1} sin (- 150^{\circ}) - F_{2} {sin 90}^{\circ}$
$= (2.0 kg) (3.0 m / s^{2}) {sin 50}^{\circ} - (10 N) sin (- 150^{\circ})$
$- (20 N) {sin 90}^{\circ}$
$= 10.4 N$ .
Vector: In unit-vector notation, we can write
${\to F}_{3} = F_{3, x} ˆ i + F_{3, y} ˆ j = (12.5 N) ˆ i - (10.4 N) ˆ j$
$\approx (13 N) ˆ i - (10 N) ˆ j$ .
We can now use a vector-capable calculator to get the magnitude and the angle of ${\to F}_{3}$ . We can also use Eq. 3-6 to obtaiin the magnitude and the angle (from the positive direction of the x axis) as
$F_{3} = \sqrt{F_{3, x}^{2} + F_{3, y}^{2}} = 16 N$
and $θ = \frac{{tan}^{- 1} (F_{3, y})}{F_{3, x}} = - 40^{\circ}$ .

Updated on:21/07/2023

A body is at rest under the action of three forces, two of which are ${\to F}_{1} = 4 ˆ i, {\to F}_{2} = 6 ˆ j$ , the third force is
A $4 ˆ i + 6 ˆ j$
B $4 ˆ i - 6 ˆ j$
C $- 4 ˆ i + 6 ˆ j$
D $- 4 ˆ i - 6 ˆ j$
Two forces ${\to F}_{1} = 500 N$ due east and ${\to F}_{2} = 250 N$ due north have their common initial point. ${\to F}_{2} - {\to F}_{1}$ is
A $250 \sqrt{5} N, {tan}^{- 1} (2) W o f N$
B $250 N, {tan}^{- 1} (2) W$ of N
CZero
D $750 N, {tan}^{- 1} (3 / 4) N o f W$
Two forces act on a 4.5 kg block resting on a frictionless surface as shown in the given figure. What is the magnitude of the horizontal acceleration of the block ?

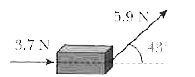A $1.8 m / s^{2}$
B $1.2 m / s^{2}$
C $0.82 m / s^{2}$
D $3.2 m / s^{2}$