Figure shows a 5.00 kg block being pulled along a frictionless floor by a cord that applies a force of constant magnitude 15.0 N but with an angle θ(t)that varies with time. When angle θ=25.0∘, at what rate is the acceleration of the block changing if (a) θ(t)=(2.00×10−2deg/s)t and (b) θ(t)=−(2.00×10−2deg/s)t ?

(a) −4.43×10−4 m/s3, (b) +4.43×10−4 m/s3
Topper's Solved these Questions
- FORCE AND MOTION - I BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION - I EXERCISE - PRACTICE QUESTIONS (Single Correct Choice Type)
36 Videos
- FORCE AND MOTION - I BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION - I EXERCISE - PRACTICE QUESTIONS (More than One Correct Choice Type)
5 Videos
- FORCE AND MOTION - I BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION - I EXERCISE - CHECKPOINT
5 Videos
- FLUIDSBOOK - RESNICK AND HALLIDAYCHAPTER - FLUIDSEXERCISE - PRACTICE QUESTIONS (Integer Type )
5 Videos
- FORCE AND MOTION-IIBOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION-IIEXERCISE - PRACTICE QUESTIONS (Integer Type)
1 Videos
Similar Questions
In Fig. 5-29, a block of mass m = 5.00 kg is pulled along a horizonttal frictionless floor by a cord that exerts a force of magnitude F = 12.0 at an angle θ=25.0∘.

Figure 5-29 A block is pulled along a horizontal floor.
(a) What is the magnitude of the block's acceleration?
View SolutionA block of mass m = 10 kg is pulled by a force F = 100 N at an angle θ=30∘ with the horizontal along a smooth horizontal surface. What is the acceleration of the block? (g=10m/s2)
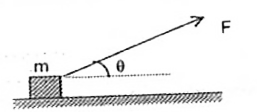
View Solution
Knowledge Check
Angular displacement (θ) of a flywheel varies with time as θ=2t+3t2 radian. The angular acceleration at t=2s is given by
A14rad/s2B18rad/s2C6rad/s2D16rad/s2The angle turned by a body undergoing circular motion depends on time as θ=θ0+θ1t+θ2r2. Then the angular acceleration of the body is
Aθ1Bθ2C2θ1D2θ2The angle turned by a body undergoing circular motion depends on time as θ=θ0+θ1t+θ2t2. Then the angular acceleration of the body is
Aθ1Bθ2C2θ1D2θ2
A wheel rotates around a stationary axis so that the rotation angle θ varies with time as θ=2t2 radian. Find the total acceleration of the point A at the rim at the moment t=0.5s If the radius of wheel is 1m.
View SolutionA 3.5 kg block is pushed along a horizontal floor by a force →F of magnitude 15 N at an angle θ=40∘ with the horizontal (Fig. 6-33). The coefficient of kinetic friction between the block and the floor is 0.25. Calculate the magnitudes of (a) the frictional force on the block from the floor and (b) the block's acceleration.

View SolutionIn Fig. 5-23a, a cord pulls a box of sea biscuits up along a frictionless plane inclined at angle θ=30.0∘. The box has mass m = 5.00 kg, and the force from the cord has magnitude T = 25.0 N. What is the box's acceleration a along the inclined plane ?
View SolutionFigure 5-50 shows Atwood's machine, in which two containers are connected by a cord (of negligible mass) passing over a frictionless pulley (also of negligible mass). At time t = 0, container 1 has mass 1.30 kg and container 2 has mass 2.80 kg, but container 1 is losing mass (through a leak) at the constant rate of 0.200 kg/s. At what rate is the acceleration magnitude of the containers changing at (a) t = 0 and (b) t = 3.00 s? (c) When does the acceleration reach its maximum value ?
View SolutionA wheel rotates around a stationary axis so that the rotation angle θ varies with time as θ=at2 where a=0.2rad/s2. Find the magnitude of net acceleration of the point A at the rim at the moment t=2.5s if the linear velocity of the point A at this moment is v=0.65m/s.
View Solution
