How many 12.5μF capacitors must be connected in parallel to store a charge of 33.0m C with a potential of 110V across the capacitors?
To solve the problem, we need to determine how many capacitors of capacitance C=12.5μF are required to store a total charge of Q=33.0mC at a voltage of V=110V.
1. Understand the relationship between charge, capacitance, and voltage:
The formula relating charge Q, capacitance C, and voltage V is given by:
Q=C⋅V
2. Convert the given values into standard units:
- Convert Q=33.0mC to coulombs:
Q=33.0mC=33.0×10−3C
- Convert C=12.5μF to farads:
C=12.5μF=12.5×10−6F
3. Calculate the total capacitance needed:
Since the capacitors are connected in parallel, the total capacitance Ctotal can be expressed as:
Ctotal=x⋅C
where x is the number of capacitors.
4. Set up the equation using the charge formula:
Substitute Ctotal into the charge formula:
Q=Ctotal⋅V=(x⋅C)⋅V
Rearranging gives:
Q=x⋅C⋅V
5. Substitute the known values into the equation:
33.0×10−3=x⋅(12.5×10−6)⋅110
6. Solve for x:
Rearranging the equation to isolate x:
x=33.0×10−3(12.5×10−6)⋅110
Calculate the denominator:
12.5×10−6⋅110=1.375×10−3
Now substitute back:
x=33.0×10−31.375×10−3≈24
7. Conclusion:
Therefore, the number of 12.5μF capacitors needed is:
x≈24
The formula relating charge Q, capacitance C, and voltage V is given by:
Q=C⋅V
- Convert Q=33.0mC to coulombs:
Q=33.0mC=33.0×10−3C
- Convert C=12.5μF to farads:
C=12.5μF=12.5×10−6F
Since the capacitors are connected in parallel, the total capacitance Ctotal can be expressed as:
Ctotal=x⋅C
where x is the number of capacitors.
Substitute Ctotal into the charge formula:
Q=Ctotal⋅V=(x⋅C)⋅V
Rearranging gives:
Q=x⋅C⋅V
33.0×10−3=x⋅(12.5×10−6)⋅110
Rearranging the equation to isolate x:
x=33.0×10−3(12.5×10−6)⋅110
Calculate the denominator:
12.5×10−6⋅110=1.375×10−3
Now substitute back:
x=33.0×10−31.375×10−3≈24
Therefore, the number of 12.5μF capacitors needed is:
x≈24
Topper's Solved these Questions
- CAPACITANCEBOOK - RESNICK AND HALLIDAYCHAPTER - CAPACITANCEEXERCISE - PRACTICE QUESTIONS (SINGLE CORRECT CHOICE TYPE)
23 Videos
- CAPACITANCEBOOK - RESNICK AND HALLIDAYCHAPTER - CAPACITANCEEXERCISE - PRACTICE QUESTIONS (MORE THAN ONE CORRECT CHOICE TYPE)
12 Videos
- CAPACITANCEBOOK - RESNICK AND HALLIDAYCHAPTER - CAPACITANCEEXERCISE - CHECKPOINTS
4 Videos
- ALL ABOUT ATOMS BOOK - RESNICK AND HALLIDAYCHAPTER - ALL ABOUT ATOMS EXERCISE - CHECKPOINT
1 Videos
- CENTER OF MASS BOOK - RESNICK AND HALLIDAYCHAPTER - CENTER OF MASS EXERCISE - Practice Questions (Integer )
4 Videos
Similar Questions
A μF capacitor C1 is charged to V0=120V. The charging battery is then removed and the capacitor is connected in parallel to an uncharged +4μF capacitor C2.
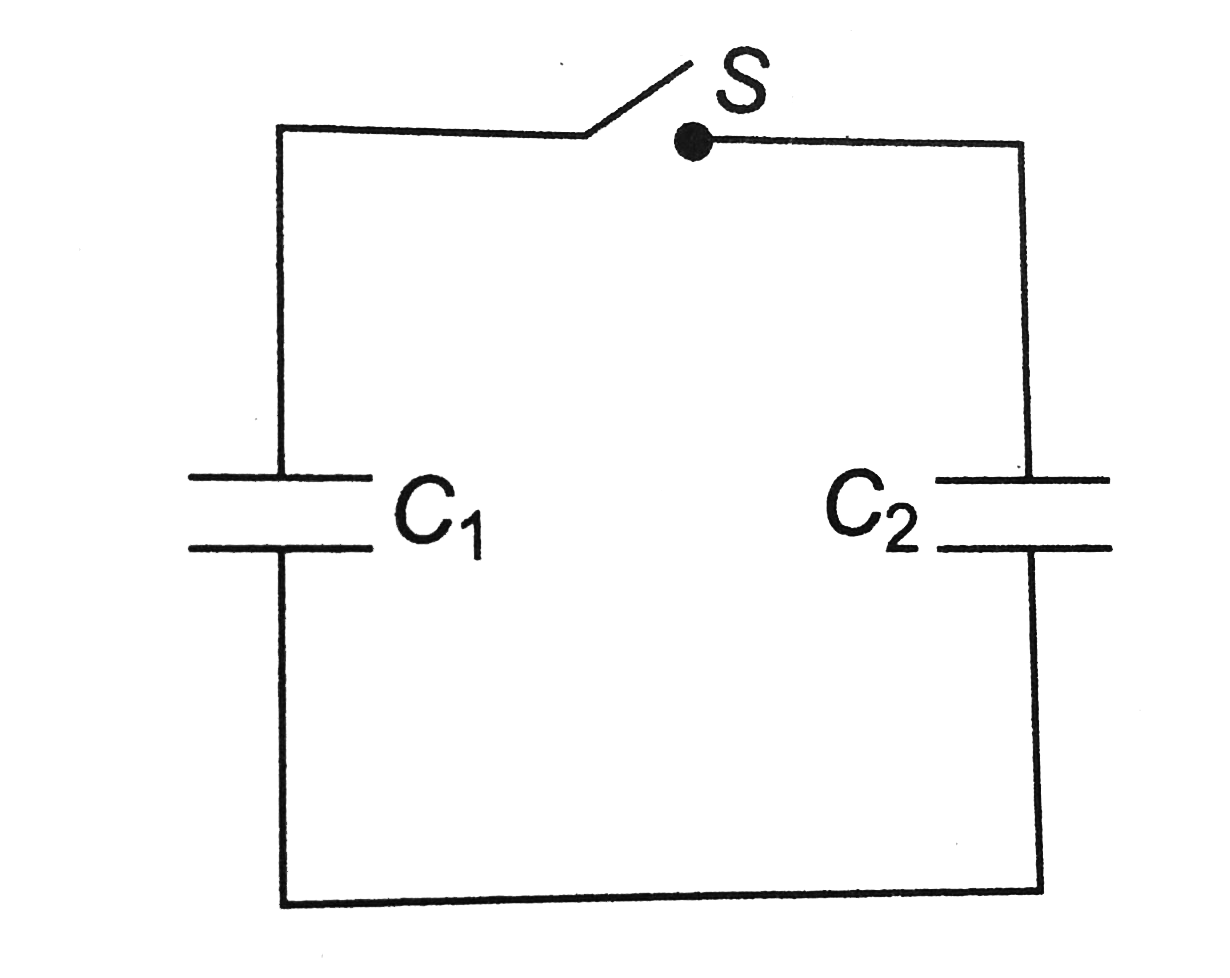
(a) what is the potential difference V across the combination?
(b) what is the stored energy before and after the switch S is closed?
View SolutionA 100pF capacitor is charged to a potential difference of 80.0V and the charging battery is disconnected. The capacitor is then connected in parallel with a second capacitor. If the potential difference across the first capacitor drops to 35.0 V what is the capacitance of this second capacitor?
View Solution
Knowledge Check
How many 1μF capacitors must be connected in parallel to store a charge of 1 C with a potential of 110 V across the capacitors?
A990B900C9090D909A capacitor or capacitance C1 is charge to a potential V and then connected in parallel to an uncharged capacitor of capacitance C2. The fianl potential difference across each capacitor will be
AC1VC1+C2BC2VC1+C2C1+C2C1D1−C2C1A capacitor or capacitance C1 is charge to a potential V and then connected in parallel to an uncharged capacitor of capacitance C2. The fianl potential difference across each capacitor will be
AC1VC1+C2BC2VC1+C2C1+C2C1D1−C2C1
When two capacitors C1andC2 are connected in parallel, the ratio of charges and potential differences across two capacitors are ____________ and ___________ respectively.
View SolutionA capacitor of unknown capacitance is connected across a battery of V volts . The charge stored in it is 360μC . When potential across the capacitor is reduced by 120 V , the charge stored in it becomes 120 μC . Calculate :
What will be the charge stored in the capacitor , if the voltage applied had increased by 120 V ?
View SolutionA capacitor of unknown capacitance is connected across a battery of V volts . The charge stored in it is 360μC . When potential across the capacitor is reduced by 120 V , the charge stored in it becomes 120 μC . Calculate :
The potential V and the unknown capacitance C .
View SolutionA capacitor of unknown capacitance is connected across a battery of V volts. The charge stored in it is 300 μC. When potential across the capacitor is reduced by 100 V, the charge stored in it becomes 100 μC. Calculate the potential V and the unknown capacitance. What will be the charge stored in the capacitor if the voltage applied had increased by 100V?
View SolutionA resistor and a capacitor are connected in series with an a.c. source. If the potential drop across the capacitor is 5 V and that across resistor is 12 V, applied voltage is
View Solution
