Figure 26-29a gives the magnitude E(x) of the electric fields that have been set up by a battery along a resistive rod of length 9.00 mm (Fig. 26-296). The vertical scale is set by Es=8.00×103V/m. The rod consists of three sections of the same material but with different radii. (The schematic diagram of Fig. 26.29b does not indicate the differencet radii). The radius of section 3 is 1.70 mm. What is the radius of (a) section 1 and (b) section 2? 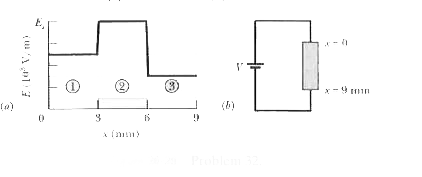
The correct Answer is:(a) 1.32 mm; (b) 104 mm
Step by step video, text & image solution for Figure 26-29a gives the magnitude E(x) of the electric fields that have been set up by a battery along a resistive rod of length 9.00 mm (Fig. 26-296). The vertical scale is set by E_(s)=8.00 xx 10^3 V//m. The rod consists of three sections of the same material but with different radii. (The schematic diagram of Fig. 26.29b does not indicate the differencet radii). The radius of section 3 is 1.70 mm. What is the radius of (a) section 1 and (b) section 2? by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CURRENT AND RESISTANCEBOOK - RESNICK AND HALLIDAYCHAPTER - CURRENT AND RESISTANCEEXERCISE - Practice Questions (Single Corret Choice Type)
39 Videos
- CURRENT AND RESISTANCEBOOK - RESNICK AND HALLIDAYCHAPTER - CURRENT AND RESISTANCEEXERCISE - Practice Questions (Linked Comprehension)
5 Videos
- CURRENT AND RESISTANCEBOOK - RESNICK AND HALLIDAYCHAPTER - CURRENT AND RESISTANCEEXERCISE - Checkpoints
6 Videos
- CIRCULAR MOTIONBOOK - RESNICK AND HALLIDAYCHAPTER - CIRCULAR MOTIONEXERCISE - CHECK POINTS
6 Videos
- ELASTICITYBOOK - RESNICK AND HALLIDAYCHAPTER - ELASTICITYEXERCISE - PRACTICE QUESTIONS (Integer Type)
3 Videos
Similar Questions
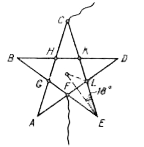
A five-pointed regular star as shown in Fig 26.3. has been soldered together from uniform wire. The resistance of the section EL is r. Find the resistance of the section FL.
View SolutionHow for does the runner whose velocity-time graph is shown in Fig. 2-25 travel in 16 s ? The figure's vertical scaling is set by vs=8.0m/s.

View Solution
Knowledge Check
Two wires of same material and length have the radii of their cross sections as r and 2r, respectively. The ratio of their resistances
A2:1B4:1C1:4D3:2Two wires of same material and length have the radii of their cross sections as r and 2r, respectively. The ratio of their resistances
A2:1B4:1C1:4D3:2The ratio of the coefficient of thermal conductivity of two different materials is 5:3. If the thermal resistance of the rod of same thickness resistance of the rods of same thickness of these materials is same, then the ratio of the length of these rods will be
A3:5B5:3C3:4D3:2
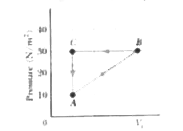
A gas within a closed chamber undergoes the cycle shown in the p-V diagram of Fig. 21-26. The horizontal scale is set by Vs=8.0m3. Calculate the net energy added to the system as heat during one complete cycle.
View SolutionIn Fig. 26-18a, a 9.00 V battery is connected to a resistive strip that consists of three sections with the same cross-sectional areas but different conductivities. Figure 26-18h gives the electric potential V(x) versus position x along the strip. The horizontal scale is set by x= 8.00 mm. Section 3 has conductivity 4.00×107(Ω.m)−1. What is the conductivity of section (a) 1 and (b) 2 ?
a.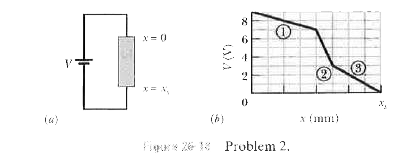
View SolutionThree rods of same material and of equal cross sectional area and length have been connected together as shown in the figure. The temperature of the junction of the rods approximately is
View SolutionTwo wires of the same material have resistances in the ratio 16:81 and lengths in the ratio 1:4. Compare their radii of cross-section.
View SolutionTwo wires of same material having length and radii in the ratio 3 : 4 and 3 : 2 respectively, are connected in parallel with a battery of 6 V, the ratio of current is
View Solution
