Twelve wires, each having resistance r, are joined to form a cube as shown in Fig. 27-18. Find the equivalent resistance between the ends of a face diagonal such as a and c.

Figure 27.18 Twelve equal resistors arc arranged in the shape of a cube. The battery is connected between points a and c.
This circuit is quite complicated and use of nodal analysis or loop law will yield a lot of equations which cantol be solved so easily. But the circuit is symmetric and symmetry considerations will help us in simplifying the circuit.
Suppose a potential difference V is applied between the points a and c so that a current i enters at a and the same current leaves at c. The current distribution is shown in Fig. 27. 1947,
By symmetry. the paths ard and ab arc equivalent and hence will carry the same current I. The path will carry the remaining current i−2i1 (using Kirchholt junction law). Similarly, at junction c, currents coming from dc and bc will be i1 each and from fc it will be i−2i1. Kirchhol.s junction law ard and it shows that current through be and dg will be zero and hence may be ignored for further analysis. Omitting these two wires, the circuit is redrawn in Fig. 27-19b.
Calculations: The wire hef and hgf are joined in parallel and have equivalent resistance (2r)(2r)/(2r + 2r)= r between h and f. This equivalent is joined in series with ah and fc giving equivalent resistance r+r+r =3r. This 3r is joined in parallel with adc (2r) and abc (2r) between a and c.
The equivalent resistance R between a and c is, therefore, given by 1R=13r+12r+12r
orR=34r
In many of the situations, we can considerably simplify the circuit by guessing the brances in which the current is the same. 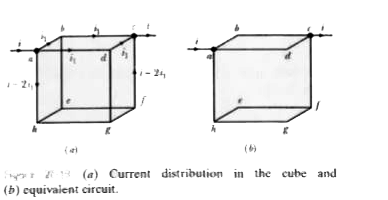
Figure 27-19 (a) Current distriution in the cube and (b) equivalent circuit.
Topper's Solved these Questions
- CIRCUITSBOOK - RESNICK AND HALLIDAYCHAPTER - CIRCUITSEXERCISE - Checkpoints
7 Videos
- CIRCUITSBOOK - RESNICK AND HALLIDAYCHAPTER - CIRCUITSEXERCISE - Problems
45 Videos
- CENTER OF MASS BOOK - RESNICK AND HALLIDAYCHAPTER - CENTER OF MASS EXERCISE - Practice Questions (Integer )
4 Videos
- CIRCULAR MOTIONBOOK - RESNICK AND HALLIDAYCHAPTER - CIRCULAR MOTIONEXERCISE - CHECK POINTS
6 Videos
Similar Questions
Twelve wire, each having resistance r, are joined to form a cube as shown in figure.Find the equivalent resistance between the end of a face diagonal such as aandc.

View SolutionTwelve wire, each having resistance r, are joined to form a cube as shown in figure.Find the equivalent resistance between the end of a face diagonal such as aandc.

View SolutionTwelve wire, each having equal resistance r, are joined to form a cube as shown in figure.Find the equivalent resistance between the diagonally opposite points a and f.

View SolutionTwelve wire, each having equal resistance r, are joined to form a cube as shown in figure.Find the equivalent resistance between the diagonally opposite points a and f.

View SolutionFive resistors are connected as shown in figure. Find the equivalent resistance between the points B and C.
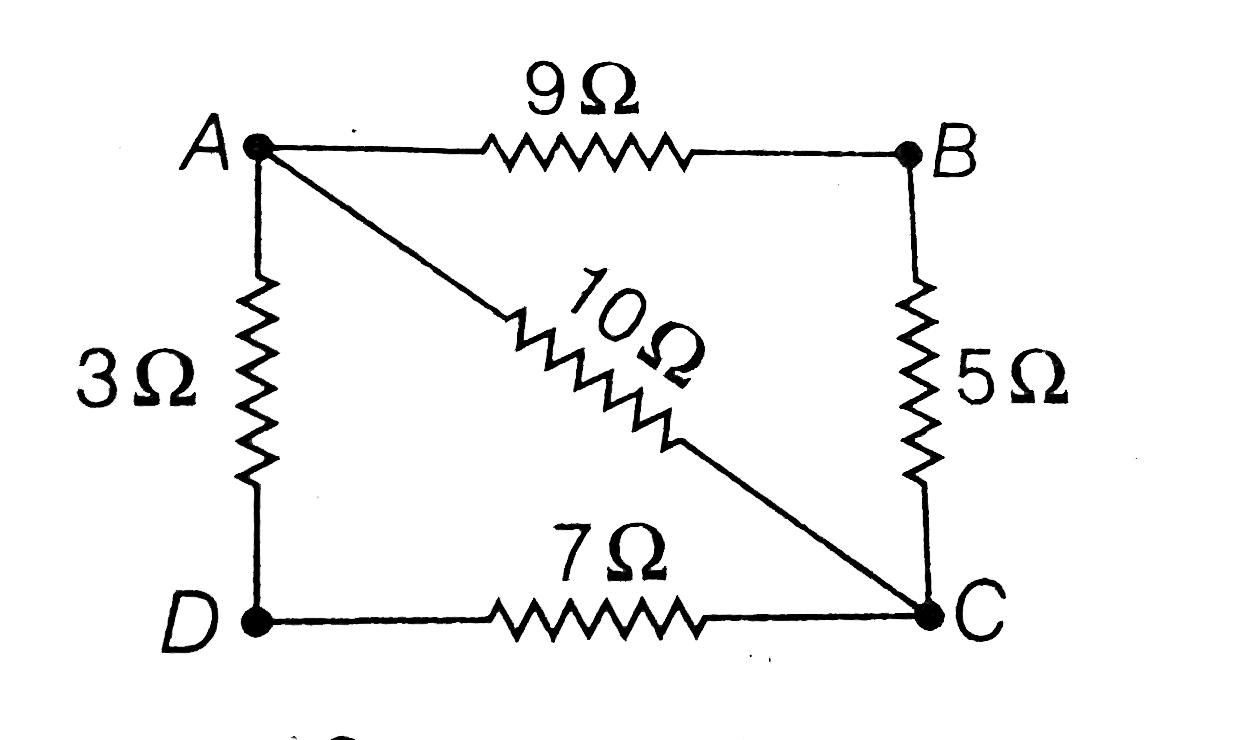
View SolutionFor the combination of resistors shown in Fig. find the equivalent resistance between the points
A and B

View SolutionFor the combination of resistors shown in Fig. find the equivalent resistance between the points
C and D

View SolutionTwelve capacitors, each having a capacitance C, are connected to form a cube . Find the equivalent capacitance between the diagonally opposite corners such as A and B.

View SolutionTwelve capacitors, each having a capacitance C, are connected to form a cube . Find the equivalent capacitance between the diagonally opposite corners such as A and B.

View Solution
Twelve indentical resistance each of resistance R are joined to form a cube as shown in figure. Find resistance of the combination across AB.
View Solution
