Twelve capacitors, each having a capacitance C, are connected to form a cube . Find the equivalent capacitance between the diagonally opposite corners such as A and B.

Suppose the points A and B are connected to a battery. The charge appearing on some of the capacitors are shown in figure. Suppose the positive termainal of the battery supplies a charge is divided on the three plates connected to A. Looking from A, the three sides of the cube have identical properties and hence, the charge will be eually distributed on the three plates. Each of the capacitors a, b and c will receive a charge Q/3. The nagative terminal of the battery supplies a charge - Q through the point B. This is again divided equally on the three plates connected to B. Each of hte capacitors d, e and f gets equal charge Q/3. Now consider the capacitors g and h. As the three plates connected to the point E form and isolated system, their total charge must be zero. the nagative plate of g and h connected to E should have a total charge Q/3. By symmetry, these two plates should have equal charges and hence each of these has a charge Q/6. The capacitors a, g and d have charges Q/3, Q/6 and Q/3 respectively. we have, <br> V_A - V_B = (V_A - V_E) + (V_E - V_F) + (V_F - V_B)<br> <br>= (Q/3)/(C ) +(Q/6)/(C ) + (Q/3)/(C) = (5Q)/(6C)<br>. or, <br>C_(eq) = (Q)/(V_A - V_B) = (5)/(6) C.
Topper's Solved these Questions
- CAPACITORSBOOK - HC VERMACHAPTER - CAPACITORSEXERCISE - Short Answer
7 Videos
- CAPACITORSBOOK - HC VERMACHAPTER - CAPACITORSEXERCISE - Objective 1
12 Videos
- CAPACITORSBOOK - HC VERMACHAPTER - CAPACITORSEXERCISE - Exercise
2 Videos
- BOHR'S MODEL AND PHYSICS OF THE ATOMBOOK - HC VERMACHAPTER - BOHR'S MODEL AND PHYSICS OF THE ATOMEXERCISE - Exercises
46 Videos
- DISPERSION AND SPECTRABOOK - HC VERMACHAPTER - DISPERSION AND SPECTRAEXERCISE - Exercises
11 Videos
Similar Questions
Suppose a charge +Q1 is given to the positive plates and a charge −Q2 to the negative plate of a capacitor. What is the "charge on the capacitor"?
View SolutionA capacitor of capacitance C is charged to a potential V. The flux of the electric field through a closed surface enclosing the capacitor is
View SolutionThe plates of a paraller-plate capacitor are made of circular discs of radii5.0cm each .If the separation between the plates is 1.0mm,What is the capacitance?
View SolutionThe bohrradius is given by a0=ε0h2πme2 verify that the KHS has dimesions of length
View SolutionA flint glass prism and a crown glass prism are to be combined in such a way that the deviation of the mean ray is zero. The refractive index of flint and crown glasses for the mean ray are 1620 and 1.518 respectively. If the refracting angle of the flint prism is 6.0∘, what would be the refracting angle of the crown prism ?
View SolutionSix equal capacitors each of capacitance C are connected as shown in the figure. The equivalent capacitance between points A and B is
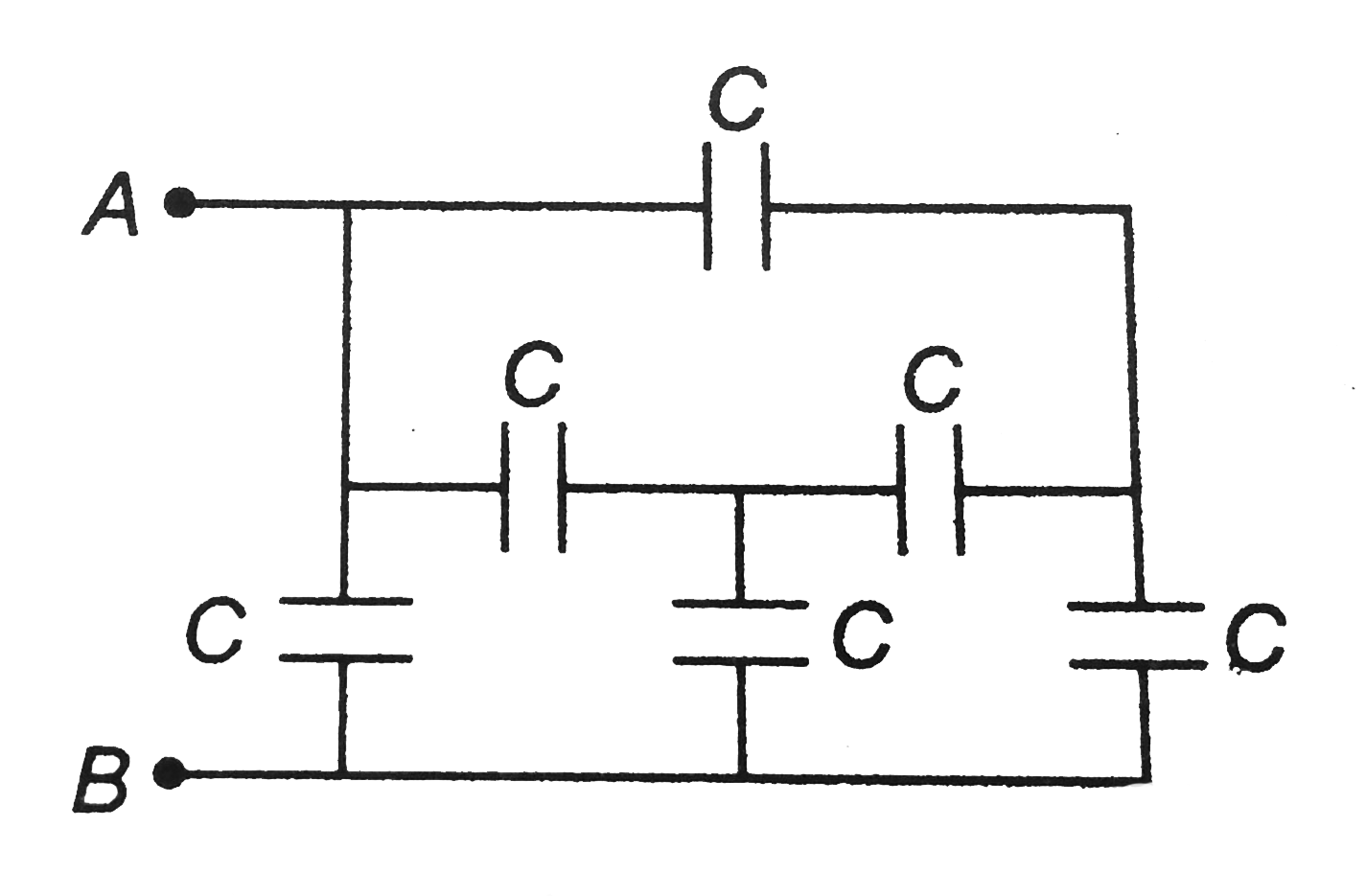
View SolutionFind the equivalent capacitance between A and B. All the capacitors have capacitance C.

View SolutionTwelve capacitors, each having capacitors, C , are joined to from a cube as shown. Find the equivalent capacitance between the ends of (a) Digitonal i.e., between A and B . (b) Face diagonal i.e., between A and C . (c) side of cube i.e., between A and D .
View SolutionFind the equivalent capacitance between terminals A & C , if each capacitor is of capacitance 4muF
View SolutionTwelve wires, each of resistance 6Ω are connected to form a cube. The effective resistance between two diagonally opposite corners of the cube is
View SolutionIf each capacitor has capacitance C, then equivalent capacitance between A and B is
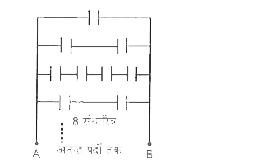
View Solutionचित्र में प्रत्येक संधारित्र की धारिता 1μF है। A व B के मध्य तुल्य धारिता ज्ञात कीजिये।
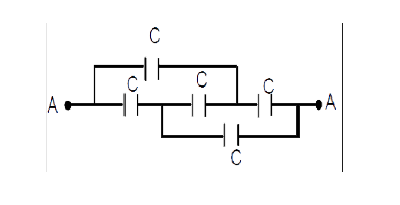
View SolutionFive equal capacitors, each with capacitance (C) are connected as shown in the adjoining fig. Then the equivalent capacitance between A and B is -
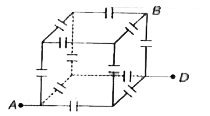
View SolutionFind the equivalent capacitance between points A and B. Capacitance of each capacitor is 2muF .
View SolutionFigure shows a combination of twelve capacitors each of capacitance C forming a cube . Find the equivalent capacitance of the combination ( a) between the diagonally opposite corners A and B of cube ( b) between the diagonally opposite corners A and D of a face of the cube .
View SolutionTwelve identical capacitors of capacitance C are connected across each edge of a cube. Find equivalent capacitance across one of the edges.
View Solution
