Find the velocity of image and the object in the vector form when the ball is just about to hit the inclined plane as shown in Fig. 3-20a. The inclined plane is at an angle of 37∘ to the horizontal.The surface of the inclined plane acts like a mirror.
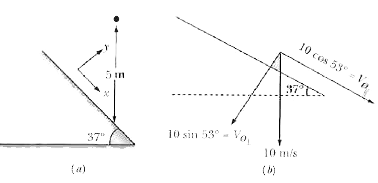
(a) An object is dropped from a height on an inclined mirror. (b) Resolving the velocity of the object in a direction parallel to an perpendicualr to the mirror.
As indicated in Eq. 33-1, the velocity of the object can be resolved in directions parallel and perpendicular to the mirror. Since the mirror is stationary, we need not bother about the motion of the mirror.
In this situation, the velocity of the striking object is in the vertical direction. Since the object moves, image moves such that the distance of the image perpendicular to the mirror remains the same as the distance of the object perpendicualr to the mirror.
Calcultaion : The velocity of the object before striking the mirror can be found by equation of kinematices.
v2=u2+2gs
v2=0+2×10×5
v=10ms
v=±10ms
Resolving this in a direction perpendicular and parallel to the mirror as shown in Fig. 33-20b, we have
VO=10cos53∘=6ms,
Vo=−10cos37∘=−10×45=−8ms
Since the inclined plane is not moving,
VI⊥=−VO⊥=8ˆj.
In the parallel direction,
VI| |=VO| |=10cos53∘=6ms
v=vxˆi+vvˆj=6ˆi+8ˆj.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - GEOMETRICAL OPTICS : REFLECTION EXERCISE - CHECKPOINT5videos
GEOMETRICAL OPTICS : REFLECTION
- BOOK - RESNICK AND HALLIDAYCHAPTER - GEOMETRICAL OPTICS : REFLECTION EXERCISE - PROBLEMS24videos
GEOMETRICAL OPTICS : REFLECTION
- BOOK - RESNICK AND HALLIDAYCHAPTER - GAUSS' LAW EXERCISE - PRACTICE QUESTIONS (INTEGER TYPE)3videos
GAUSS' LAW
- BOOK - RESNICK AND HALLIDAYCHAPTER - GEOMETRICAL OPTICS : REFRACTIONEXERCISE - Practice questions(Integers)4videos
GEOMETRICAL OPTICS : REFRACTION
Similar Questions
A ball is projected from point A with velocity 20 m/s prependicular to the inclined plane as shown in figure. What is the range of the ball on the inclined plane ?
 View Solution
View SolutionA ball is projected from point A with velocity 10ms−1 perpendicular to the inclined plane as shown in figure. Range of the ball on the inclined plane is
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
a particle is projected down on inclined plane with a velocity of 21m/s at an angle of 60∘ with the horizontal its range on the inclined plane inclined at an angle of 30∘ with the horizontal is
A21dmB2.1dmC30dmD6dm - Question 2 - Select One
a particle is projected down on inclined plane with a velocity of 21m/s at an angle of 60∘ with the horizontal its range on the inclined plane inclined at an angle of 30∘ with the horizontal is
A21dmB2.1dmC30dmD6dm - Question 3 - Select One
A ball is projected from point A with velocity 10ms−1 perpendicular to the inclined plane as shown in figure. Range of the ball on the inclined plane is
 A403mB203mC123mD603m
A403mB203mC123mD603m
In figure, the angle of inclination of the inclined plane is 30∘. Find the horizontal velocity V0 so that the particle hits the inclined plane perpendicularly.
 . View Solution
. View SolutionA particle is projected with a velocity of 20 m/s at an angle of 30∘ to an inclined plane of inclination 30∘ to the horizontal. The particle hits the inclined plane at an angle 30∘, during its journey. The time of flight is -
View SolutionA ball is projected from point A with velocity 10ms−1 perpendicular to the inclined plane as shown in figure. Range of the ball on the inclined plane is
 View Solution
View SolutionOn an inclined plane of inclination 30∘, a ball is thrown at angle of 60∘ with the horizontal from the foot of the incline with a velocity of 10√3ms−1. Then the ball will hit the inclined plane in
View SolutionIn figure, the angle of inclination of the inclined plane is 30∘. Find the horizontal velocity V0 so that the particle hits the inclined plane perpendicularly.
 . View Solution
. View Solution

