A plane mirror, reflecting a ray of incident light, is rotated through an angle θ about an axis through the point of incidence in the plane of the mirror perpendicular to the plane of incidence, then
The reflected ray does not rotate
The reflected ray rotates through an angle θ
The reflected ray rotates through an angle 2θ
The incident ray is fixed
The correct Answer is:C, D
To solve the problem of a plane mirror reflecting a ray of incident light that is rotated through an angle θ, we can follow these steps:
1. Understand the Initial Setup:
- Consider a plane mirror positioned vertically. A ray of light strikes the mirror at an angle φ with respect to the normal (the line perpendicular to the surface of the mirror).
- According to the law of reflection, the angle of incidence (φ) is equal to the angle of reflection (φ).
2. Identify the Rotation of the Mirror:
- The mirror is rotated through an angle θ about an axis that passes through the point of incidence and is perpendicular to the plane of incidence.
- This rotation changes the orientation of the mirror but does not change the point of incidence.
3. Determine the New Angle of Reflection:
- After the mirror is rotated, the normal to the mirror at the point of incidence also rotates. The new angle of the normal with respect to the original position is now θ.
- Therefore, the angle between the incident ray and the new normal is now φ + θ.
4. Calculate the New Angle of Reflection:
- Since the angle of incidence is now φ + θ, the angle of reflection will also be φ + θ (by the law of reflection).
5. Determine the Total Deviation of the Reflected Ray:
- The deviation (Δ) of the reflected ray can be calculated as the difference between the original angle of reflection and the new angle of reflection.
- The original angle of reflection was φ, and the new angle of reflection is φ + θ.
- Therefore, the total deviation is given by:
Δ=(ϕ+θ)−ϕ=θ
Final Answer:
The deviation of the reflected ray when the mirror is rotated through an angle θ is θ.
- Consider a plane mirror positioned vertically. A ray of light strikes the mirror at an angle φ with respect to the normal (the line perpendicular to the surface of the mirror).
- According to the law of reflection, the angle of incidence (φ) is equal to the angle of reflection (φ).
- The mirror is rotated through an angle θ about an axis that passes through the point of incidence and is perpendicular to the plane of incidence.
- This rotation changes the orientation of the mirror but does not change the point of incidence.
- After the mirror is rotated, the normal to the mirror at the point of incidence also rotates. The new angle of the normal with respect to the original position is now θ.
- Therefore, the angle between the incident ray and the new normal is now φ + θ.
- Since the angle of incidence is now φ + θ, the angle of reflection will also be φ + θ (by the law of reflection).
- The deviation (Δ) of the reflected ray can be calculated as the difference between the original angle of reflection and the new angle of reflection.
- The original angle of reflection was φ, and the new angle of reflection is φ + θ.
- Therefore, the total deviation is given by:
Δ=(ϕ+θ)−ϕ=θ
The deviation of the reflected ray when the mirror is rotated through an angle θ is θ.
Topper's Solved these Questions
- GEOMETRICAL OPTICS : REFLECTION BOOK - RESNICK AND HALLIDAYCHAPTER - GEOMETRICAL OPTICS : REFLECTION EXERCISE - PRACTICE QUESTIONS (Linked Comprehension)
2 Videos
- GEOMETRICAL OPTICS : REFLECTION BOOK - RESNICK AND HALLIDAYCHAPTER - GEOMETRICAL OPTICS : REFLECTION EXERCISE - PRACTICE QUESTIONS (Integer Type)
3 Videos
- GEOMETRICAL OPTICS : REFLECTION BOOK - RESNICK AND HALLIDAYCHAPTER - GEOMETRICAL OPTICS : REFLECTION EXERCISE - PRACTICE QUESTIONS (single correct choice type)
27 Videos
- GAUSS' LAW BOOK - RESNICK AND HALLIDAYCHAPTER - GAUSS' LAW EXERCISE - PRACTICE QUESTIONS (INTEGER TYPE)
3 Videos
- GEOMETRICAL OPTICS : REFRACTIONBOOK - RESNICK AND HALLIDAYCHAPTER - GEOMETRICAL OPTICS : REFRACTIONEXERCISE - Practice questions(Integers)
4 Videos
Similar Questions
A plane mirror reflecting a ray of incident light is rotated through an angle q about an axis through the point of incidence in the plane of the mirror perpendicular to the plane of incidence, then
(1) The reflected ray rotates through an angle 2q
(2) The incident ray is fixed
(3) The reflected ray does not rotate
(4) The reflected ray rotates through an angle q
View SolutionFor a fixed incident light ray, if the mirror be rotated through and angle θ (about an axis which lies in the plane of mirror and perpendicular to the plane of incidence), show that the reflected ray turns through an angle 2θ in same sense.
View Solution
Knowledge Check
A plane mirror reflecting a ray of incident light is rotated through an angle of 30∘ about an axis through the point of incidence in the plane of the mirror and perpendicular to the plane of incidence then
Athe incident ray is fixedBthe reflected ray rotates through an angle θCthe reflected ray rotates through an angle θ/2Dthe reflected ray rotates through an angle of 2θWhen a plane mirror is rotated through an angle θ then the reflected ray turns through the angle 2θ then the size of the image
AIs doubledBIs halvedCRemins the sameDBecomes infiniteA plane mirror reflects a beam of light to from a real image. The incident beam is
AparallelBconvergentCdivergentDany one of the above
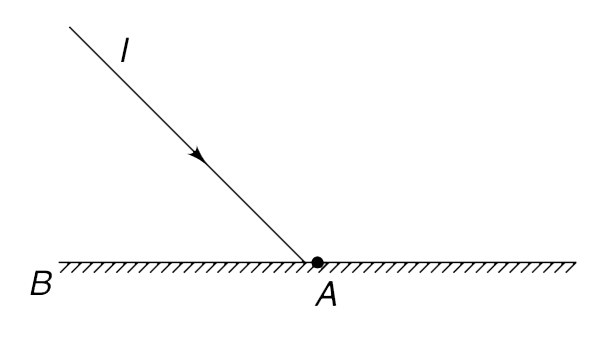
I is a ray incident on a plane mirror. Keeping the incident ray fixed, the mirror is rotated by an angle θ about an axis passing through A perpendicular to the plane of the Fig. show that the refracted ray rotates through an angle 2θ. Does your answer differ if the mirror is rotated about an axis passing through B?
View SolutionA ray of light is incident on a plane mirror placed horizontally. When the mirror is rotated through an angle 30∘ the reflected ray is found to be directed along the vertical. Determine the angle of incidence at the initial position of the mirror.
View SolutionShow that a ray of light reflected from a plane mirror rotates througha an angle 2θ when the
mirror is rotated through an angle θ about its axis perpendicular to both the incident ray and
the normal to the surface.
View SolutionA ray of light is incident on a plane mirror, making an angle 'q' with the surface of the mirror. Arrange the following steps in sequential order to calculate the angle between the incident light ray and the reflected light ray.
(A) Draw a normal line on the plane mirror at the point of incidence of the light ray.
(B) Note down the angle between the plane mirror and the incident light ray.
(C) The sum of the angle of incidence and the angle between the plane mirror and the incident ray is 90∘.Determine the angle of incidence.
(D) From the laws of reflection, the angle of incidence is equal to the angle of reflection. Then the sum of the angle of incidence and the angle of reflection gives the angle between the incident light ray and the reflected light ray.
View SolutionA ray of light is incident on a plane mirror, making an angle 'q' with the surface of the mirror. Arrange the following steps in sequential order to calculate the angle between the incident light ray and the reflected light ray.
(A) Draw a normal line on the plane mirror at the point of incidence of the light ray.
(B) Note down the angle between the plane mirror and the incident light ray.
(C) The sum of the angle of incidence and the angle between the plane mirror and the incident ray is 90∘.Determine the angle of incidence.
(D) From the laws of reflection, the angle of incidence is equal to the angle of reflection. Then the sum of the angle of incidence and the angle of reflection gives the angle between the incident light ray and the reflected light ray.
View Solution
