Assume a proton is a sphere of radius R≈1 fm. Two protons are fired at each other with the same kinetic energy. K
a. What must K be if the paticles are brought to rest by their mutual Coulomb repulsion when they are just touching each other? We can take this value of K as a representative measure of the height of the Colulomb barrier.
To solve the problem, we need to determine the kinetic energy K required for two protons to come to rest due to their mutual Coulomb repulsion when they are just touching each other. Here’s a step-by-step solution:
Step 1: Understand the scenario
Two protons are fired at each other with the same kinetic energy K. When they touch, they come to rest due to the repulsive electrostatic force between them.
Step 2: Apply conservation of energy
The total initial kinetic energy of the system is equal to the total potential energy at the point of contact (when they come to rest). The conservation of energy can be expressed as:
Total Initial Kinetic Energy=Total Final Potential Energy
Since both protons have kinetic energy K, the total initial kinetic energy is:
2K
When they are just touching, the potential energy U due to their Coulomb repulsion is given by:
U=14πϵ0q1q2r
where q1 and q2 are the charges of the protons and r is the distance between their centers.
Step 3: Substitute values
For protons, the charge q is:
q=1.6×10−19 C
The distance r when they are just touching is twice the radius of a proton:
r=2R=2×1 fm=2×10−15 m
Step 4: Calculate the potential energy
Substituting the values into the potential energy formula:
U=14πϵ0(1.6×10−19)22×10−15
Using ϵ0≈8.85×10−12 C2/N m2:
U=(1.6×10−19)24π(8.85×10−12)(2×10−15)
Step 5: Calculate K
Setting the total initial kinetic energy equal to the potential energy:
2K=U
Thus,
K=U2
Step 6: Solve for K
Calculating U:
U=(1.6×10−19)24π(8.85×10−12)(2×10−15)
Calculating this gives:
U≈5.75×10−14 J
Then,
K=5.75×10−142≈2.875×10−14 J
Step 7: Convert to electron volts
To convert joules to electron volts (1 eV = 1.6×10−19 J):
K≈2.875×10−141.6×10−19≈360 keV
Final Answer
The required kinetic energy K for the protons to come to rest due to their mutual Coulomb repulsion when they are just touching each other is approximately:
K≈360 keV
Two protons are fired at each other with the same kinetic energy K. When they touch, they come to rest due to the repulsive electrostatic force between them.
The total initial kinetic energy of the system is equal to the total potential energy at the point of contact (when they come to rest). The conservation of energy can be expressed as:
Total Initial Kinetic Energy=Total Final Potential Energy
Since both protons have kinetic energy K, the total initial kinetic energy is:
2K
When they are just touching, the potential energy U due to their Coulomb repulsion is given by:
U=14πϵ0q1q2r
where q1 and q2 are the charges of the protons and r is the distance between their centers.
For protons, the charge q is:
q=1.6×10−19 C
The distance r when they are just touching is twice the radius of a proton:
r=2R=2×1 fm=2×10−15 m
Substituting the values into the potential energy formula:
U=14πϵ0(1.6×10−19)22×10−15
Using ϵ0≈8.85×10−12 C2/N m2:
U=(1.6×10−19)24π(8.85×10−12)(2×10−15)
Setting the total initial kinetic energy equal to the potential energy:
2K=U
Thus,
K=U2
Calculating U:
U=(1.6×10−19)24π(8.85×10−12)(2×10−15)
Calculating this gives:
U≈5.75×10−14 J
Then,
K=5.75×10−142≈2.875×10−14 J
To convert joules to electron volts (1 eV = 1.6×10−19 J):
K≈2.875×10−141.6×10−19≈360 keV
The required kinetic energy K for the protons to come to rest due to their mutual Coulomb repulsion when they are just touching each other is approximately:
K≈360 keV
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - THE NUCLEUSEXERCISE - CHECKPOINT5videos
THE NUCLEUS
- BOOK - RESNICK AND HALLIDAYCHAPTER - THE NUCLEUSEXERCISE - PROBLEMS66videos
THE NUCLEUS
- BOOK - RESNICK AND HALLIDAYCHAPTER - THE KINETIC THEORY OF GASESEXERCISE - PRACTICE QUESTIONS72videos
THE KINETIC THEORY OF GASES
- BOOK - RESNICK AND HALLIDAYCHAPTER - UNITS AND MEASUREMENT EXERCISE - PRACTICE QUESTIONS (MATRIX-MATCH)11videos
UNITS AND MEASUREMENT
Similar Questions
Calculate the Coulomb barrier height for two Li nuclei that are fired at each other with the same initial kinetic energy K.
View SolutionCalculate the height of the potential barrier for a head on collision of two deuterons.
(Hint : The height of the potential barrier is given by the Coulomb repulsion between the two deuterons when they just touch each other. Assume that they can be taken as hard spheres of radius 2.0 fm.)View Solution
Knowledge Check
- Question 1 - Select One
Scienists are working hard to develop inclear fusion reactor Nocies of heavy hydrogen, _(1)2H , known as deuteron and denoted by D, can be thought of as a candidate for fusion rector . The D−D reaction is _(1)2H+21H→12He+n+e≠rgy in the core of fasion reactor a gas of heavy hydrogen of _(1)2H nucles and electrons is know as plasma . The nuclei move randonity in the reactor to take place Unally , the temperature in the reactor core are too ligh and to natrual will can be used to confine the to pleama for a time l_(0) before the particles by away from the case if n is the denasity (number volume ) of determines , the productnt0is called Lavson number in one of the criteria , a reactor is termed successful if Lawson number is greater then 5×1014s/cm2
it may be helpfull to use the following botczmann constant
λ=8.6×10−5eV/k,e24πs0=1.44×10−9eVm
Assume that two deuteron nuclei in the core of fasion reactor at temperacture energy T are moving toward each other, each with kinectic energy 1.5kT , whenn the seperation between them is large enogh to leglect coulomb potential energy . Also neglate any interaction from other particle in the core . The minimum temperature T required for them to reach a separation of 4×10−15m is in the rangeA1.0×109K<T<2.0×109KB2.0×109K<T<3.0×109KC3.0×109K<T<4.0×109KD4.0×109K<T<5.0×109K - Question 2 - Select One
Assertion: When two protons are brought closer to each other against their electrostatic repulsion then their combined mass becomes slightly more than their total mass.
Reason: If we bring two similar charges closer to each other from infinity then work is needed to be done against electrostatic repulsion. Mechanical work against electrostatic repulsion gets stored in the system as electric energy. We know that E=mc2, hence due to an increase in energy of the system, equivalent mass of the system increases.AIf both assertion and reason are correct and reason is a correct explanation of the assertion .BIf both assertion and reason are correct but reason is not the correct explanation of assertionCIf assertion is correct but reason is incorrectDIf both assertion and reason are incorrect. - Question 3 - Select One
In hexagonal systems of crystals, a frequently encountered arrangement of atoms is described as a hexagonal prism.Here, the top and bottom of the cell are regular hexagons and three atoms are sandwiched in between them.A space-fitting model of this structure, called hexagonal closed-packed (HCP), is constitution of a sphere on a flat surface surrounded in the same plane by six identical spheres as closely as possible Three spheres are then placed over the first layer so that they touch each other and represent the second layer.Each one of these three spheres touches three spheres of the bottom layer.Finally, the second layer is covered with third layer that is identical to the bottom layer in relative position.Assume radius of even sphere to be 'r'.
In hcp lattice, if a plane is drawn parallel to layers A and B at a distance c8 above the layer B, it passes through centres of x tetrahedral and y octahedral voids.A plane parallel to layer A at a distance c8 just below it passes through centres of p tetrahedral and q octahedral voids.Find (x+y+p+q) c is the cell parameter of hcp lattice, the vertical edge length.
 A10B9C6D14
A10B9C6D14
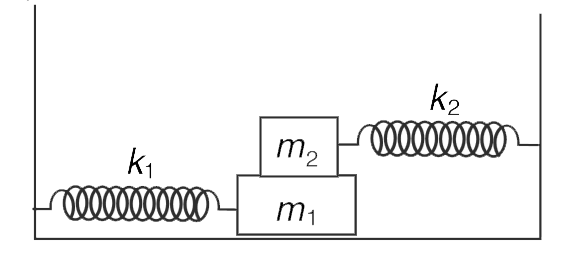
(i) In the shown arrangement, both springs are relaxed. The coefficient of friction between m2 and m1 is μ. There is no friction between m1 and the horizontal surface. The blocks are displaced slightly and released. They move together without slipping on each other.
(a) If the small displacement of blocks is x then find the magnitude of acceleration of m2. What is time period of oscillations ?
(b) Find the ratio m1m2 so that the frictional force on m2 acts in the direction of its displacement from the mean position.
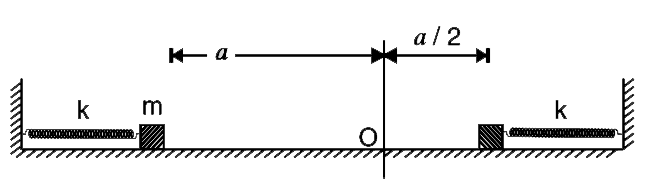
(ii) Two small blocks of same mass m are connected to two identical springs as shown in fig. Both springs have stiffness K and they are in their natural length when the blocks are at point O. Both the blocks are pushed so that one of the springs get compressed by a distance a and the other by a/2. Both the blocks are released from this position simultaneously. Find the time period of oscillations of the blocks if - (neglect the dimensions of the blocks)
(a) Collisions between them are elastic.
(b) Collisions between them are perfectly inelastic.
 View Solution
View SolutionA stationary body explodes in to four identical fragments such that three of them fly mutually perpendicular to each other, each with same KE(E0). The energy of explosion will be
View SolutionAssume that the protons in a hot ball of protons each have a kinetic energy equal to kT, where k is the Boltzmann constant and T is the absolute temperature. If T=1×107K, what (approximately) is the least separation 98.905 94 u any two protons can have?
View SolutionAn accelration produces a narrow beam of protons, each having an initial speed of v0. The beam is directed towards an initially uncharges distant metal sphere of radius R and centered at point O. The initial path of the beam is parallel to the axis of the sphere at a distance of (R/2) from the axis, as indicated in the diagram.
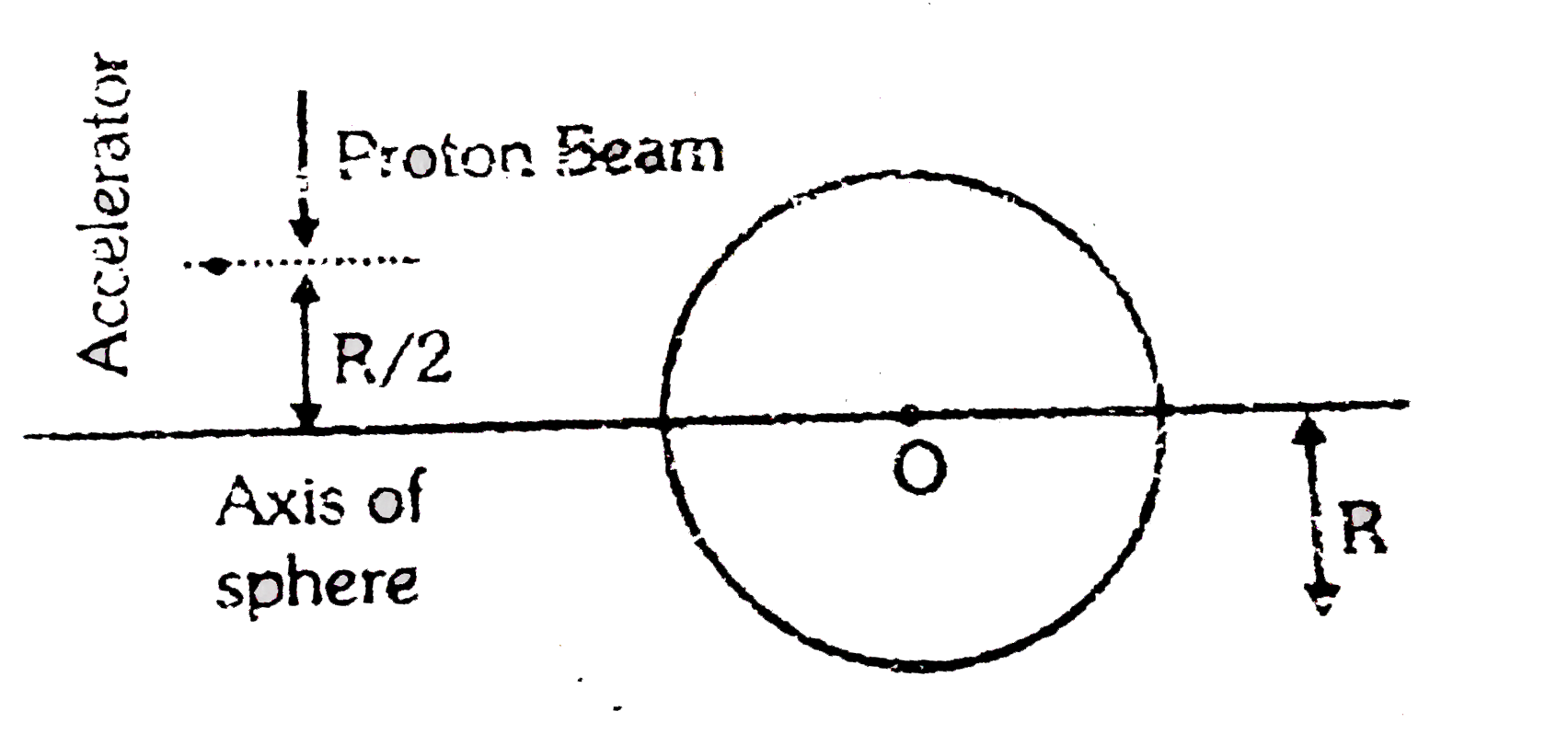
The protons in the beam that collide with the sphere will cause it to becomes charged. The subsequentpotential field at the accelerator due to the sphere can be neglected. The angular momentum of a particle is defined in a similar way to the moment of a force. It is defined as the moment of its linear momentum, linear replacing the force. We may assume the angular momentum of a proton about point O to be conserved. Assume the mass of the proton as mP and the charge on it as e. Given that the potential of the sphere increases with time and eventually reaches a constant velue.
If the initial kinetic energy of a proton is 2.56keV, then the final potential of the sphere isView SolutionAn accelration produces a narrow beam of protons, each having an initial speed of v0. The beam is directed towards an initially uncharges distant metal sphere of radius R and centered at point O. The initial path of the beam is parallel to the axis of the sphere at a distance of (R/2) from the axis, as indicated in the diagram.

The protons in the beam that collide with the sphere will cause it to becomes charged. The subsequentpotential field at the accelerator due to the sphere can be neglected. The angular momentum of a particle is defined in a similar way to the moment of a force. It is defined as the moment of its linear momentum, linear replacing the force. We may assume the angular momentum of a proton about point O to be conserved. Assume the mass of the proton as mP and the charge on it as e. Given that the potential of the sphere increases with time and eventually reaches a constant velue.
After a long time, when the potential of the sphere reaches a constant value, the trajectory of proton is correctly sketched as
 View Solution
View Solution

