Assume two copper rods A and B are connected to each other at one end. Lengths of the rods ar equal.
Radii of cross section of A and B are 2 mm and 4 mm respectively. If the current density in A is 9×105A/m2 then calculate the current density in B.
To solve the problem, we need to find the current density in rod B (denoted as JB) given the current density in rod A (JA) and the dimensions of both rods.
1. Understand the relationship between current densities and areas:
Since rods A and B are connected, the current flowing through both rods must be the same. Therefore, we can use the relationship:
IA=IB
where IA and IB are the currents through rods A and B respectively.
2. Express current in terms of current density:
The current I can be expressed in terms of current density J and cross-sectional area A:
I=J×A
Thus, we can write for rods A and B:
IA=JA×AA
IB=JB×AB
3. Set the currents equal:
Since IA=IB, we can set the two equations equal to each other:
JA×AA=JB×AB
4. Calculate the cross-sectional areas:
The cross-sectional area A of a rod is given by:
A=πr2
For rod A (with radius rA=2mm=2×10−3m):
AA=π(2×10−3)2=π(4×10−6)=4π×10−6m2
For rod B (with radius rB=4mm=4×10−3m):
AB=π(4×10−3)2=π(16×10−6)=16π×10−6m2
5. Substitute the known values into the equation:
We know JA=9×105A/m2. Now substituting the values into the equation:
9×105×(4π×10−6)=JB×(16π×10−6)
6. Simplify the equation:
Cancel π and 10−6 from both sides:
9×105×4=JB×16
36×105=JB×16
7. Solve for JB:
JB=36×10516=2.25×105A/m2
Final Answer:
The current density in rod B is JB=2.25×105A/m2.
Since rods A and B are connected, the current flowing through both rods must be the same. Therefore, we can use the relationship:
IA=IB
where IA and IB are the currents through rods A and B respectively.
The current I can be expressed in terms of current density J and cross-sectional area A:
I=J×A
Thus, we can write for rods A and B:
IA=JA×AA
IB=JB×AB
Since IA=IB, we can set the two equations equal to each other:
JA×AA=JB×AB
The cross-sectional area A of a rod is given by:
A=πr2
For rod A (with radius rA=2mm=2×10−3m):
AA=π(2×10−3)2=π(4×10−6)=4π×10−6m2
For rod B (with radius rB=4mm=4×10−3m):
AB=π(4×10−3)2=π(16×10−6)=16π×10−6m2
We know JA=9×105A/m2. Now substituting the values into the equation:
9×105×(4π×10−6)=JB×(16π×10−6)
Cancel π and 10−6 from both sides:
9×105×4=JB×16
36×105=JB×16
JB=36×10516=2.25×105A/m2
The current density in rod B is JB=2.25×105A/m2.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - PRACTICE PROBLEMS
71 Videos
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - CONCEPTUAL QUESTIONS
35 Videos
- ATOMS BOOK - MODERN PUBLICATIONCHAPTER - ATOMS EXERCISE - Chapter Practice Test
16 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - CHAPTER PRACTICE TEST
15 Videos
Similar Questions
A current of 4.8 A is flowing in a copper wire of cross-sectional area 3×10−4m2. Find the current density in the wire.
View SolutionA rod PQ of length 1.05m having negligible mass is supported at its ends by two wires one of stell (wire A), and the other of aluminium (wire B) of equal lengths as shown in fig. The cross-sectional areas of wires A and B are 1.0mm2 and 2.0mm2 respectively. At what point along the rod a load W be suspended in order to produce
(a) equal stress, (b) equal strains in both steel an aluminium.
(Ysteel=200GPa,Yaluminium=70GPa)
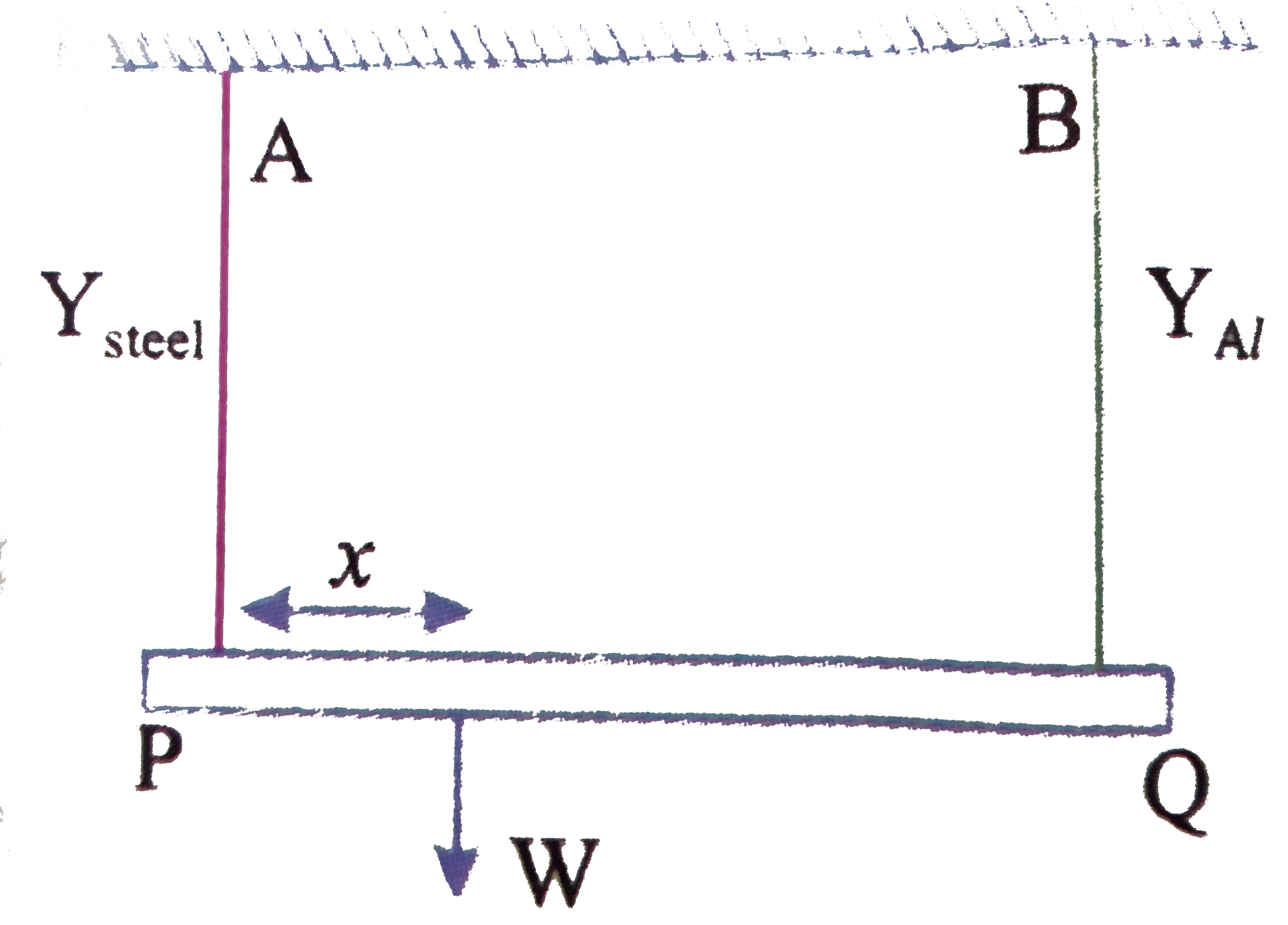
View Solution
Knowledge Check
A conductor-carries a current of 50μA If the area of cross-section of the conductor is 50mm2, then value of the current density in Amis
A0.5B1C101D3/10A curent of 50μAflows through a conductor of cross-section 50mm2 . The current density in A−m−2 is
A10−2B10−1C1D10Consider the figure, cross-sectional area of consider at A and B is 2a and a respectively. Current density at A and B are given by JA and JB then JA/JB is
 A12B2C1D4
A12B2C1D4
Drift speed of electrons, when 1.5 A of current flows in a copper wire of cross setion mm2 , is v. If the electron density in copper is 9×1028/m3 the value of v in mm/s close to (Take charge of electron to be =1.6×10−19C)
View SolutionDrift speed of electrons, when 1.5 A of current flows in a copper wire of cross setion mm2 , is v. If the electron density in copper is 9×1028/m3 the value of v in mm/s close to (Take charge of electron to be =1.6×10−19C)
View SolutionA metallic wire A of radius 1 mm is joined at one end with another metallic wire B of radius 2 mm .
when a battery is connected between two free ends of this composite wire, a currents of 20 A flows through it.
Calculate the currents density in wire A and also calculate the drift speed of electrons in wire B , if material of B has 9×1029 free electrons per unit volume.
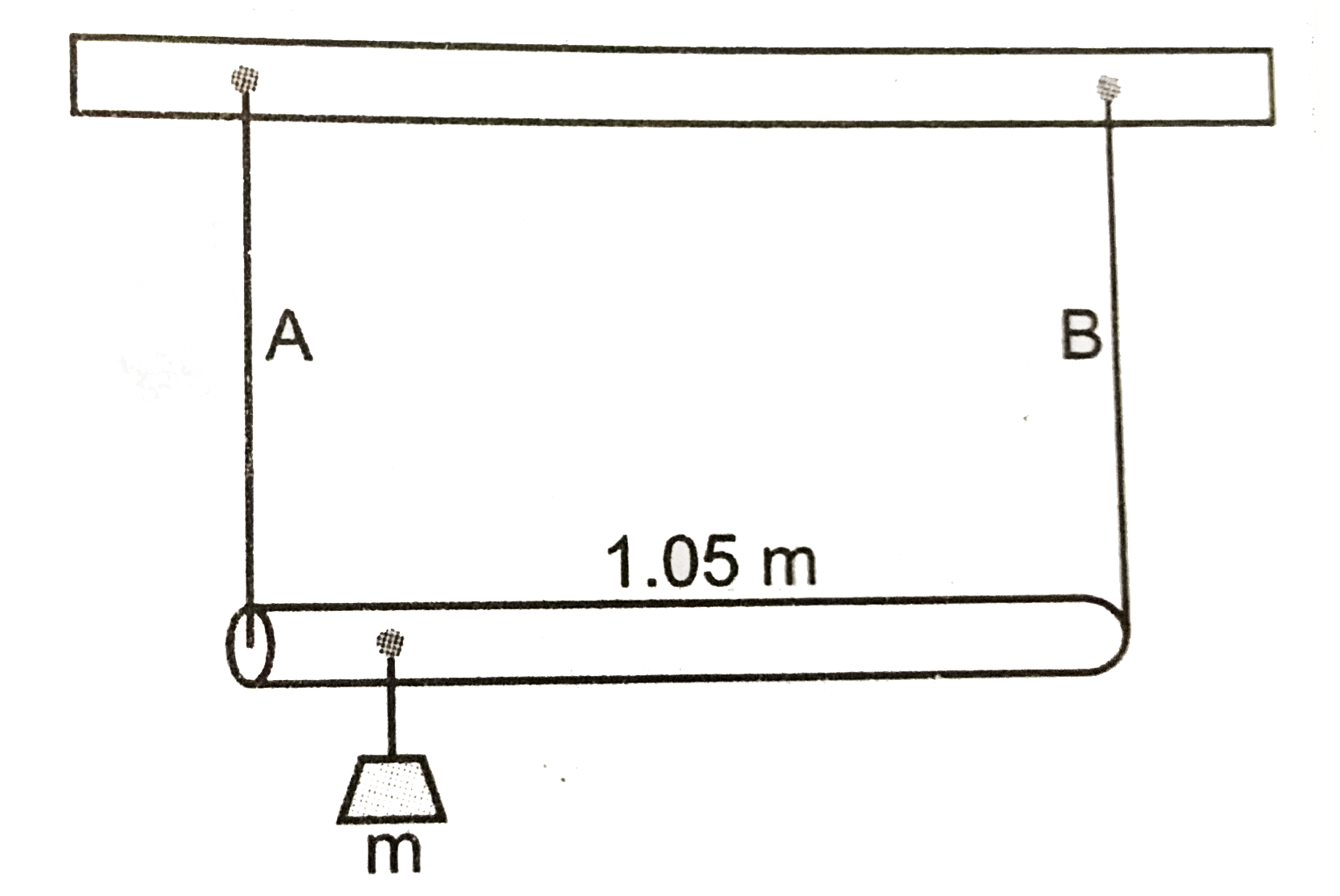
View SolutionA rod of length 1.05 m having negliaible mass is supported at its ends by two wires of steel (wire A) and aluminium (wire B) of equal lengths as shown in fig. The cross-sectional area of wire A and B are 1mm2 and 2mm2, respectively . At what point along the rod should a mass m be suspended in order to produce (a) equal stresses and (b) equal strains in both steel and aluminium wires. Given,
Ysteel=2×1011Nm−2andY−(aluminium)=7.0×1010N−2
View SolutionA current of 5A is passing through a metallic wire of cross-section area 4×10−6m2. If the density of the charge carries in the wire is 5×1036/m3, the drift velocity of the electrons is.
View Solution
