Three cells of emfs ɛ1=1.5V,ɛ2=2.0vandɛ3=3.0V having internal resistances r1=0.3Ωr2=0.4Ωandr3=0.6Ω respectively are connected in parallel . Find out the equivalent emf and the equivalent resistance of a cell which can replace this combination.
To find the equivalent EMF and equivalent resistance of the three cells connected in parallel, we can follow these steps:
Step 1: Calculate the Equivalent EMF
The formula for the equivalent EMF (E_eq) in a parallel circuit with internal resistances is given by:
EeqReq=E1r1+E2r2+E3r3
Where:
- E1=1.5V, r1=0.3Ω
- E2=2.0V, r2=0.4Ω
- E3=3.0V, r3=0.6Ω
Substituting the values:
EeqReq=1.50.3+2.00.4+3.00.6
Calculating each term:
1.50.3=5,2.00.4=5,3.00.6=5
Adding these values together:
EeqReq=5+5+5=15
Step 2: Calculate the Equivalent Resistance
The equivalent resistance Req for resistances in parallel is given by:
1Req=1r1+1r2+1r3
Substituting the values:
1Req=10.3+10.4+10.6
Calculating each term:
10.3≈3.33,10.4=2.5,10.6≈1.67
Adding these values together:
1Req=3.33+2.5+1.67=7.5
Now, taking the reciprocal to find Req:
Req=17.5≈0.1333Ω
Final Results
- The equivalent EMF Eeq=2V
- The equivalent resistance Req≈0.1333Ω
The formula for the equivalent EMF (E_eq) in a parallel circuit with internal resistances is given by:
- E1=1.5V, r1=0.3Ω
- E2=2.0V, r2=0.4Ω
- E3=3.0V, r3=0.6Ω
The equivalent resistance Req for resistances in parallel is given by:
- The equivalent EMF Eeq=2V
- The equivalent resistance Req≈0.1333Ω
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - CONCEPTUAL QUESTIONS
35 Videos
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - TOUGH AND TRICKY PROBLEMS
23 Videos
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - Chapter Practice Test
15 Videos
- ATOMS BOOK - MODERN PUBLICATIONCHAPTER - ATOMS EXERCISE - Chapter Practice Test
16 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - CHAPTER PRACTICE TEST
15 Videos
Similar Questions
Three cells of emf, ε1=1.5V,ε2=2.0Vandε3=3.0V having internal resistance r1=0.30Ω,r2=0.4Ωandr3=0.6Ω respectively are connected in parallel. Find out the equivalent emf and the equivalent resistance of a cell which can replace this combination.
View SolutionTwo cells of emfs 1.5 V and 2.0 V having internal resistances 0.2Ω and 0.3Ω respectively are connected in parallel. Calculate the emf and internal resistance of the equivalent cell.
View Solution
Knowledge Check
Two batteries of emfs 2 V and 1 V of internal resistances 1Ωand2Ω respectively are connected in parallel. The effective emf of the combination is
A32VB53VC35VD2VA circuit consists of three batteries of emf E1 = 1 V, E2=2VandE3=3V and internal resistances 1Ω,2Ωand1Ω respectively which are connected in parallel as shown in the figure. The potential difference between points P and Q is
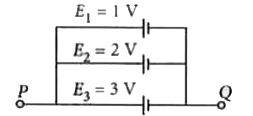 A1.0VB2.0VC2.2VD3.0V
A1.0VB2.0VC2.2VD3.0VTwo resistor of resistance R1=(6±0.09)Ω and R2=(3±0.09)Ω are connected in parallel the equivalent resistance R with error (in Ω)
AR=(2±0.04)BR=(2±0.05)CR=(9±0.18)DR=(2±0.18)
Two cells of emfs 1.5 V and 2.0v having internal resistance 0.2Σ and 0.3 Σ respectively are connected in parallel . Calculate the emf and internal resistance of the equivalent cell .
View SolutionTwo cells of emf ε1 and ε2 having internal resistances r1 and r2 respectively are connected in parallel as shown in Fig. Deduce the expressions for the equivalent emf and equivalent internal resistance of a cell which can replace the combination between the pointsB1 and B2 .

View SolutionTwo cells of emfs 1.5 V and 2.0v having internal resistance 0.2Σ and 0.3 Σ respectively are connected in parallel . Calculate the emf and internal resistance of the equivalent cell .
View SolutionTwo resistances R1=100±3ΩandR2=200±4Ω are connected in series . Find the equivalent resistance of the series combination.
View SolutionTwo cells of 1.5 V and 2 V , having internal resistances of 1Ω and 2Ω respectively, are connected in parallel so as to read the current in the same direction through an external resistance of 5Ω . The current in the external resistance will be
View Solution
