Two cells of emfs 1.5 V and 2.0v having internal resistance 0.2Σ and 0.3 Σ respectively are connected in parallel . Calculate the emf and internal resistance of the equivalent cell .
To solve the problem of finding the equivalent emf and internal resistance of two cells connected in parallel, we can follow these steps:
Step 1: Identify the given values
- For Cell 1:
- Emf (E1) = 1.5 V
- Internal resistance (r1) = 0.2 Ω
- For Cell 2:
- Emf (E2) = 2.0 V
- Internal resistance (r2) = 0.3 Ω
Step 2: Calculate the equivalent emf (E_eq)
When two cells are connected in parallel, the equivalent emf (E_eq) can be calculated using the formula:
Eeq=E1⋅r2+E2⋅r1r1+r2
Substituting the values:
Eeq=(1.5V⋅0.3Ω)+(2.0V⋅0.2Ω)0.2Ω+0.3Ω
Step 3: Calculate the numerator
Calculating the numerator:
Eeq=(1.5⋅0.3)+(2.0⋅0.2)0.5
=0.45+0.40.5
=0.850.5
=1.7V
Step 4: Calculate the equivalent internal resistance (r_eq)
The equivalent internal resistance (r_eq) for cells in parallel can be calculated using the formula:
1req=1r1+1r2
Substituting the values:
1req=10.2+10.3
Step 5: Calculate the individual fractions
Calculating the individual fractions:
1req=5+103=5+3.33=8.33
Step 6: Find r_eq
Taking the reciprocal to find r_eq:
req=18.33≈0.12Ω
Final Result
Thus, the equivalent emf and internal resistance of the combined cell are:
- Equivalent Emf (E_eq) = 1.7 V
- Equivalent Internal Resistance (r_eq) ≈ 0.12 Ω
- For Cell 1:
- Emf (E1) = 1.5 V
- Internal resistance (r1) = 0.2 Ω
- For Cell 2:
- Emf (E2) = 2.0 V
- Internal resistance (r2) = 0.3 Ω
When two cells are connected in parallel, the equivalent emf (E_eq) can be calculated using the formula:
Eeq=E1⋅r2+E2⋅r1r1+r2
Substituting the values:
Eeq=(1.5V⋅0.3Ω)+(2.0V⋅0.2Ω)0.2Ω+0.3Ω
Calculating the numerator:
Eeq=(1.5⋅0.3)+(2.0⋅0.2)0.5
=0.45+0.40.5
=0.850.5
=1.7V
The equivalent internal resistance (r_eq) for cells in parallel can be calculated using the formula:
1req=1r1+1r2
Substituting the values:
1req=10.2+10.3
Calculating the individual fractions:
1req=5+103=5+3.33=8.33
Taking the reciprocal to find r_eq:
req=18.33≈0.12Ω
Thus, the equivalent emf and internal resistance of the combined cell are:
- Equivalent Emf (E_eq) = 1.7 V
- Equivalent Internal Resistance (r_eq) ≈ 0.12 Ω
Topper's Solved these Questions
- XII BOARDSBOOK - XII BOARDS PREVIOUS YEARCHAPTER - XII BOARDSEXERCISE - Section -C
10 Videos
- XII BOARDSBOOK - XII BOARDS PREVIOUS YEARCHAPTER - XII BOARDSEXERCISE - Section-D
18 Videos
- XII BOARDSBOOK - XII BOARDS PREVIOUS YEARCHAPTER - XII BOARDSEXERCISE - Section -A
15 Videos
- SAMPLE PAPER 2019BOOK - XII BOARDS PREVIOUS YEARCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION D
6 Videos
Similar Questions
Two cells of emfs 1.5 V and 2.0 V having internal resistances 0.2Ω and 0.3Ω respectively are connected in parallel. Calculate the emf and internal resistance of the equivalent cell.
View SolutionTwo cells of emfs 1.5 V and 2.0v having internal resistance 0.2Σ and 0.3 Σ respectively are connected in parallel . Calculate the emf and internal resistance of the equivalent cell .
View Solution
Knowledge Check
Two batteries of emfs 2 V and 1 V of internal resistances 1Ωand2Ω respectively are connected in parallel. The effective emf of the combination is
A32VB53VC35VD2VTwo cells of e.m.f. 2.5 V and 2.0 V having internal resistance of 1Ω and 2Ω respectively are connected in parallel with similar poles connected together so as to send the current in the same direction through an external resistance of 2Ω. The current in the external resistance is
A0.87 AB1.29 AC1.00 AD2.29 A
Two cells of 1.5 V and 2 V , having internal resistances of 1Ω and 2Ω respectively, are connected in parallel so as to read the current in the same direction through an external resistance of 5Ω . The current in the external resistance will be
View SolutionTwo cells of emf 2ε and ε and internal resistance 2r and r respectively, are connected in parallel. Obtain the expressions for the equivalent emf and the internal resistance of the combination.
View SolutionThe emf of a cell having internal resistance is
View SolutionIf three cell are connected in parallel then equivalent emf……. and equivalent internal resistance is …..
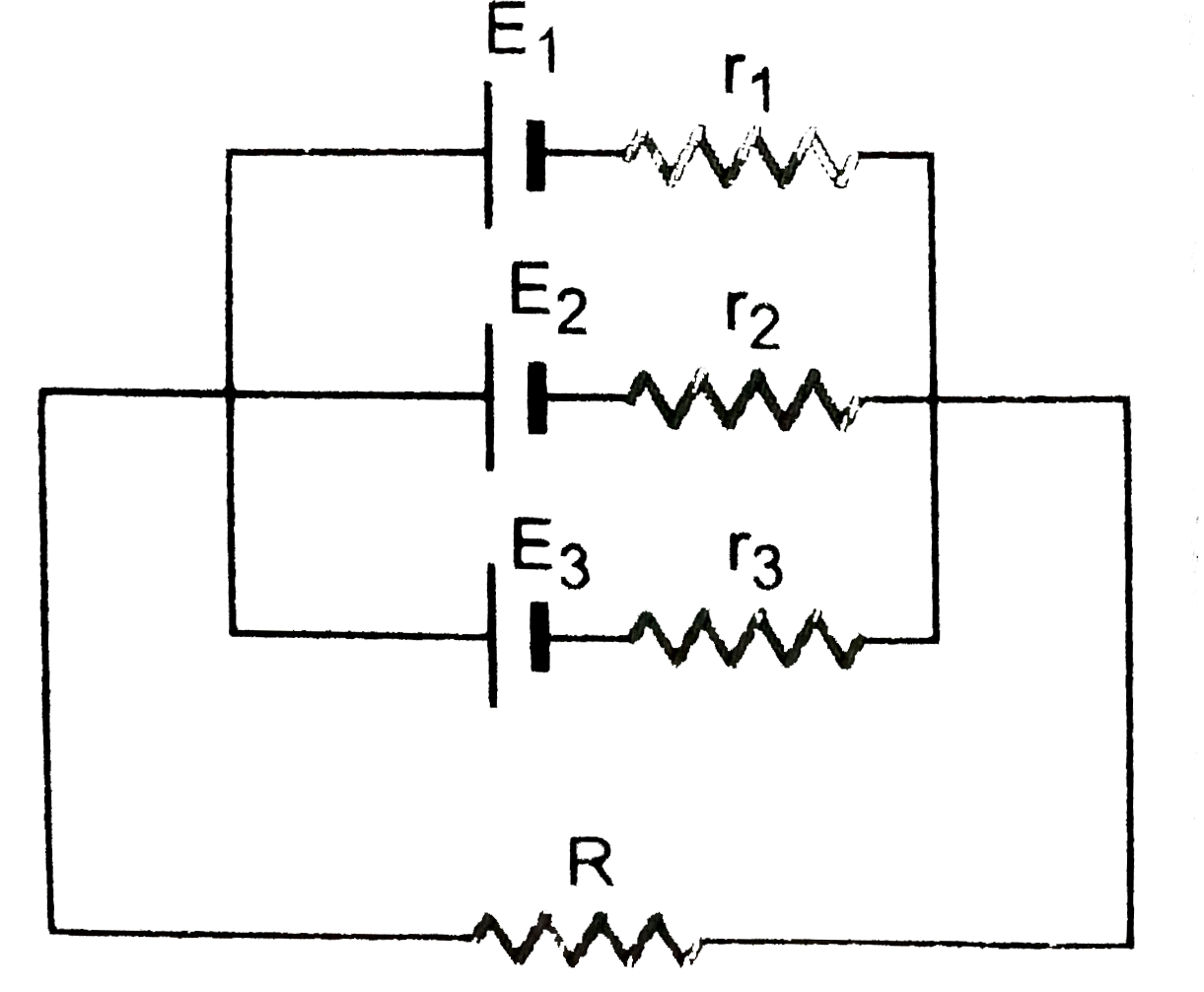
View SolutionTwo cells of emf ε1 and ε2 having internal resistances r1 and r2 respectively are connected in parallel as shown in Fig. Deduce the expressions for the equivalent emf and equivalent internal resistance of a cell which can replace the combination between the pointsB1 and B2 .

View SolutionThree cells of emfs varepsilon_1=1.5 V, varepsilon_2=2.0 v and varepsilon_3 =3.0 V having internal resistances r1=0.3Ωr2=0.4Ωandr3=0.6Ω respectively are connected in parallel . Find out the equivalent emf and the equivalent resistance of a cell which can replace this combination.
View Solution
