Determine the current in each branch of the following network:

Text Solution
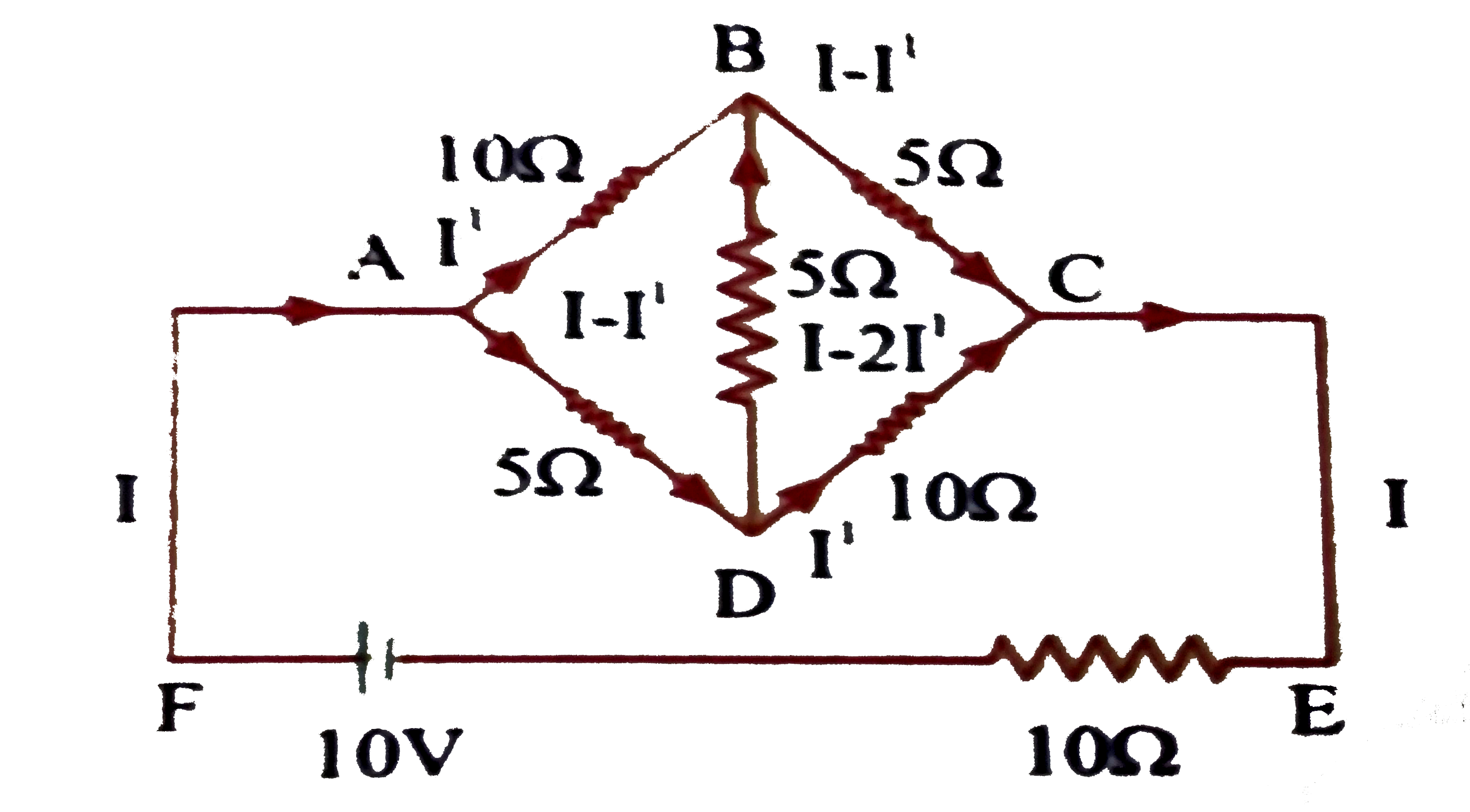
The currents flowing through various branches of the circuit are labeled as shown in the figure given below. Applying Kirchhoff.s loop law to various closed loops. For loop ABDA: −10I1−5I3+5I2=0
⇒10I1+5I3−5I2=0
⇒2I1+I3−I2=0 ...(i)
For loop BCDAB: −5(I1−I3)+10(I2+I3)+5I2−10I1=0
⇒5(I1−I3)−10(I2+I3)−5I2+10I1=0
⇒15I1−15I3−15I2=0
⇒I1−I3−I2=0 ..(ii)
Adding (i) and (ii), we get
2I1+I3−I2+I1−I3−I2=0
⇒3I1−2I2=0 ...(iii)
Applying kirchoff.s loop rule to loop ADCFA, we get −5I2−(I2+I3)10+10−10I=0
⇒5I2+10(I2+I3)+10I=10
Applying KCL at point A, I=I1+I2
⇒5I2+10(I2+I3)+10(I1+I2)=10
⇒10I1+25I2+10I3=10
⇒2I1+5I2+2I3=2 ..(iv)
Multiplying (i) by 2 and subtracting (iv) from it, we get
4I1+2I3−2I2−(2I1+5I2+2I3)=−2
⇒2I1−7I2=−2
⇒6I1−21I2=−6 ...(v)
Multiplying (iii) by 2 and subtracting from (v), we get
6I1−21I2−(6I1−4I2)=−6
−17I2=−6
I2=617A
∴ Current through branch AD=617A
Using (iii), 3I1=2I2=2×617=1217
⇒I1=417A
∴ Current through AB=417A
Total current in the circuit, I=I1+I2
=617+417=1017A
Total current in the circuit:
I=I1+I2=617+417=1017A
From (i), 2×417−617+I3=0
⇒817−617+I3=0
⇒217+I3=0
⇒I3=−217A
∴ Current through BD=−217A
Also, current through BC=I1−I3
=417+217=617A
And current through DC=I2+I3
=−617−(−217)=−417A
|
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - NCERT SOLVED (NCERT Additional Exercises)
11 Videos
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - NCERT SOLVED (NCERT Exemplar Problems Subjective Questions)(Very Short Answers Type Questions)
10 Videos
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - TOUGH AND TRICKY PROBLEMS
23 Videos
- ATOMS BOOK - MODERN PUBLICATIONCHAPTER - ATOMS EXERCISE - Chapter Practice Test
16 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - CHAPTER PRACTICE TEST
15 Videos
Similar Questions
Determine the current in each branch of the network shown in Fig.
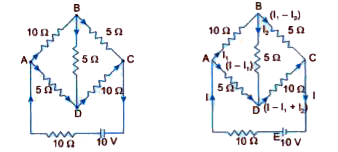
View Solution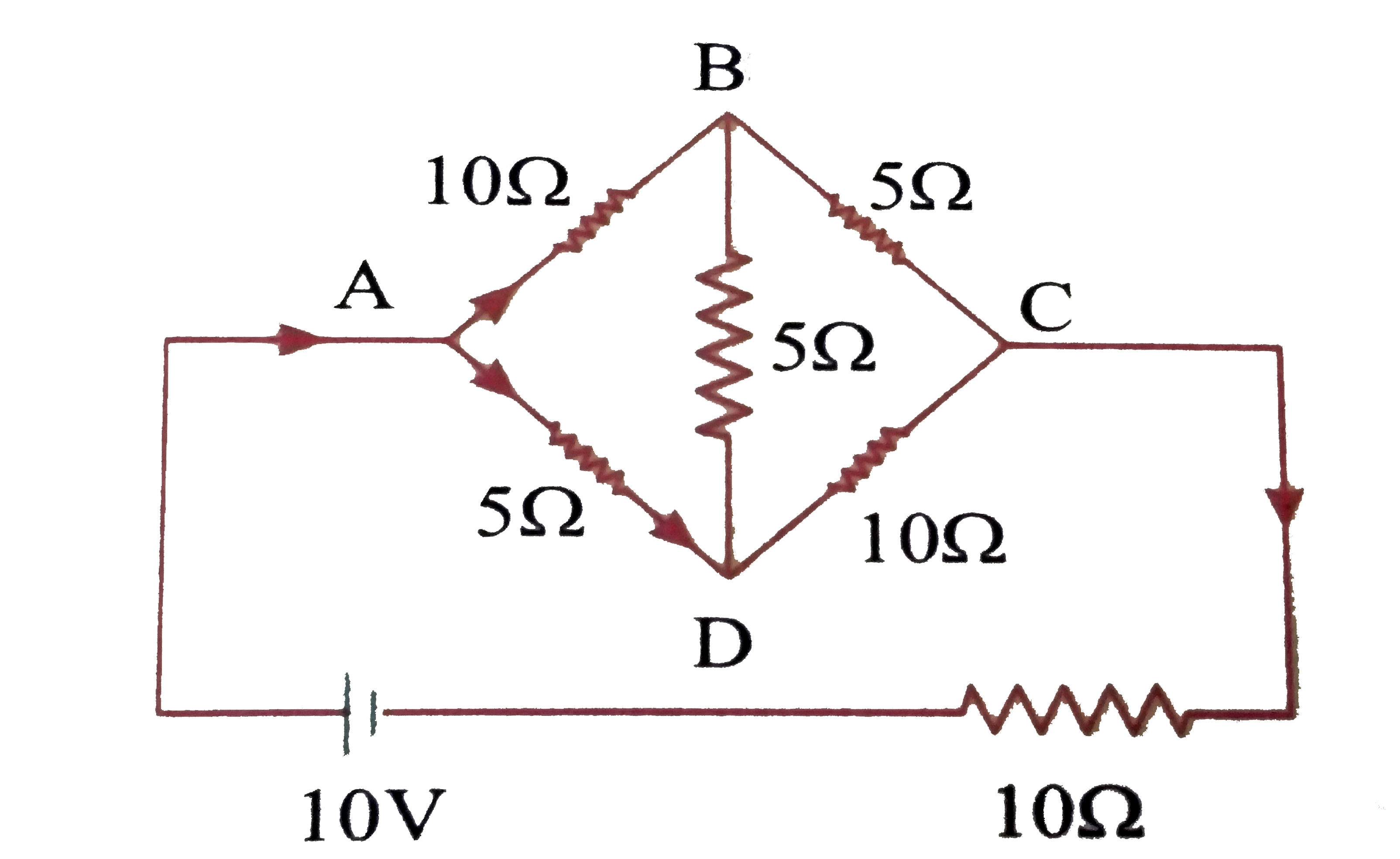
Determine the current in each branch of the network shown in fig.
View SolutionDetermine the current in each branch of the network shown in figure.
View SolutionDetermine the current in each branch of the network shown in figure.

View Solution

Determine the current in each branch of the network shown in fig.
View SolutionDetermine the current in each branch of the network shown in Fig. 3.24

View Solution
Find the current in every branch ?
View Solution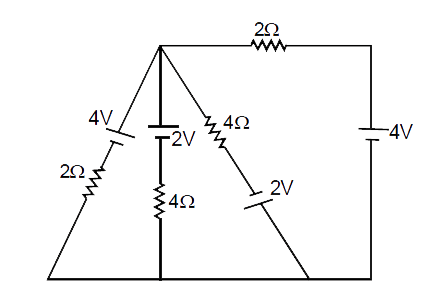
Find the current in every branch ?
View Solution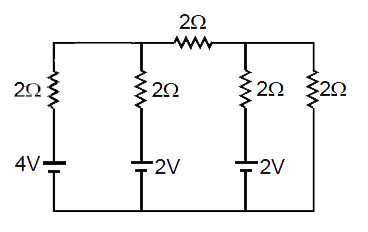
Find the current in every branch ?
View SolutionFind the current in each branches of the circuit.
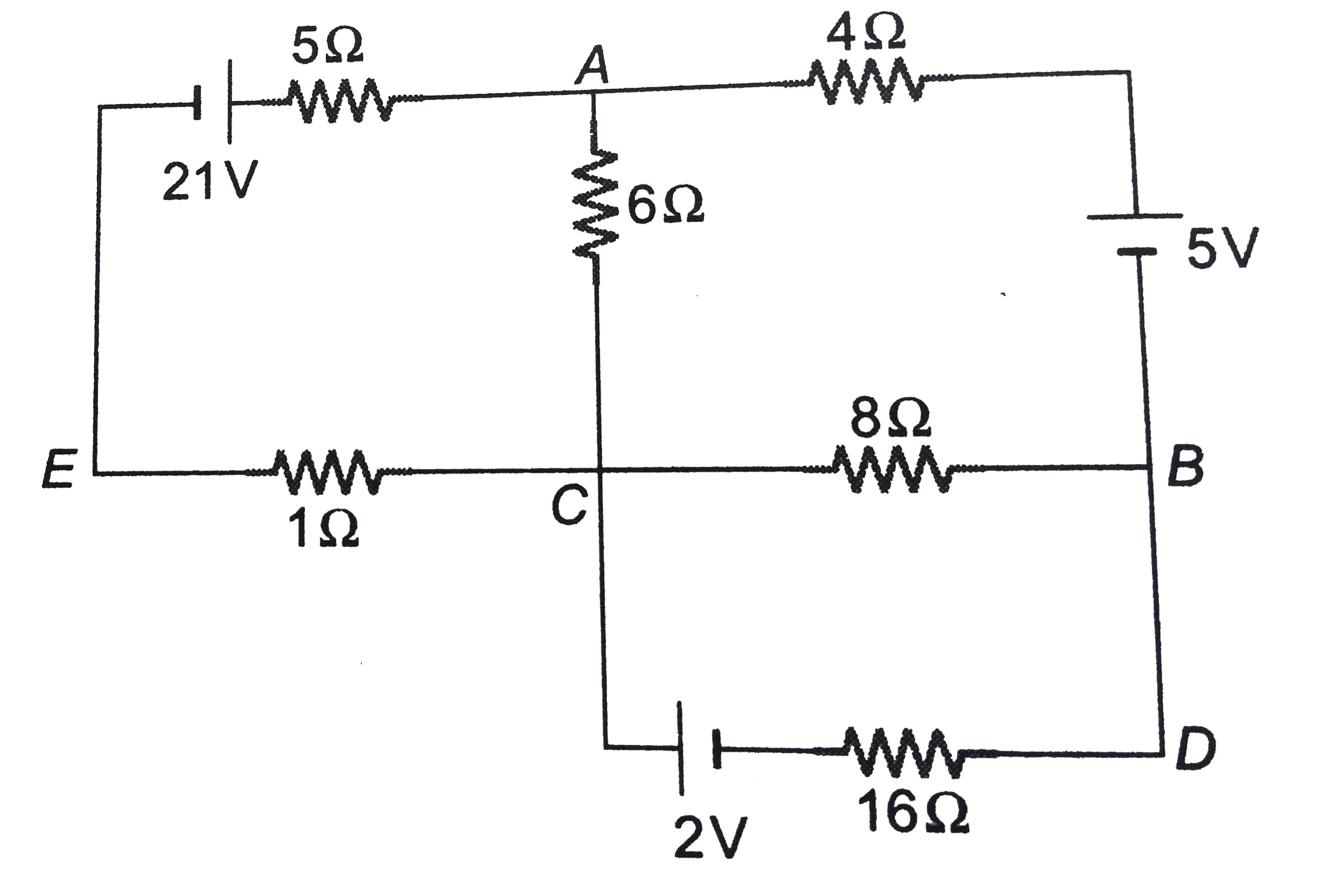
View Solution
