(a) Given n resistors each of the resistance R, how will you combine them to get the
(i) maximum,
(ii) minimum effective resistance? What is the ratio of the maximum to minimum resistance?
(b) Given the resistances of 1Ω,2Ω,and3Ω, how will we combine them to get an equivalent resistance of
(i) 113Ω (ii) (i) 115Ω (iii) (i) 611Ω?
(c ) Determine the equivalent resistance of the following networks shown in fig. (a) and (b):

(a) (i) The effective resistance of the combination will be maximum when all the resistors are connected in series.

In series, the total resistance of n resistors, each of resistance R will be
RS=nR
(ii) The effective resistance of the combination will be minimum when all the resistors are connected in parallel.

In parallel, the total resistance of n resistors, each of resistance R will be
RP=Rn
The ratio of maximum to minimum resistance will be given by
RSRP=nR×nR=n2
(b) (i) To obtain an equivalent resistance of 113Ω join 1Ωand2Ω resistances in parallel and this combination is then connected in series with 3Ω resistance as shown in figure.

The effective resistance of parallel combination of resistance 1Ωand2Ω is 1RP=11+12
⇒RP=1×21+2=23Ω
Now RP when connected in series with 3Ω resistance will give equivalent resistance as below:
RS=3+23=113Ω
(ii) To obtain an equivalent resistance of 115Ω join 2Ωand3Ω resistance in parallel and this combination is then connected in series with 1Ω resistance as shown in figure.

The effective resistance of parallel combination of resistances 1Ωand2Ω is 1RP=12+13
⇒RP=2×32+3=65Ω
Now RP when connected in series with 1Ω resistance will give equivalent resistance as below:
RS=1+65=115Ω
(iii) To obtain an equivalent resistance of 6Ω, all resistance should be connected in series. The equivalent resistance of series combination of resistances 1Ω,2Ωand3Ω is
RS=1Ω+2Ω+3Ω=6Ω
(iv) To obtain an equivalent resistance of 611Ω all resistances should be connected in parallel. The equivalent resistance of parallel combinatin of resistances 1Ω,2Ωand3Ω is:
1RP=11+12+13
=6+3+26=116
⇒RP=611Ω
(c ) For the network in figure (a) We will divide the network in four units each of arrangement as shown below.

In the above unit, two 1Ω resistances are connected in series and in parallel to this combination and two resistances are connected in series. Equivalent resistance for series combination of 1Ω resistances =1+1=2Ω
Equivalent resistance for series combination of 2Ω resistances =2+2=4Ω
The arrangement will be equivalent to one shown below:
The equivalent resistance of this arrangement will be given by

1RP=12+14
=2+14=34
RP=43Ω
This will be the equivalent resistance of one unit of the given network. Since four such units are connected in a series combination in the network, the total resistance of the network will be given by:
RS=43+43+43+43=163Ω
For the network in figure (b) For the network given below, if we connect a battery across the two end points of the network, the same current will flow through all the resistors. So, in the given network, the resistances are connected in series.

The total resistance of the network will be given by:
RS=R+R+R+R+R=5R
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - NCERT SOLVED (NCERT Exemplar Problems Subjective Questions)(Very Short Answers Type Questions)
10 Videos
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - NCERT SOLVED (NCERT Exemplar Problems Subjective Questions)(Short Answers Type Questions)
6 Videos
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - NCERT SOLVED (NCERT Textbook Exercises)
13 Videos
- ATOMS BOOK - MODERN PUBLICATIONCHAPTER - ATOMS EXERCISE - Chapter Practice Test
16 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - CHAPTER PRACTICE TEST
15 Videos
Similar Questions
Given n resistors each of resistance R, how will you combine them to get the (i) maximum, and (ii) minimum effective resistance? What is the ratio of the maximum to minimum resistance?
View SolutionGiven n resistors each of resistance R, how will you combine them to get the (i) maximum (ii) minimum effective resistance ? What is the ratio of the maximum to minimum resistance ?
View Solution
Knowledge Check
If you are provided three resistance 2Ω,3Ω and 6Ω. How will you connect them so as to obtain the equivalent resistance of 4Ω
A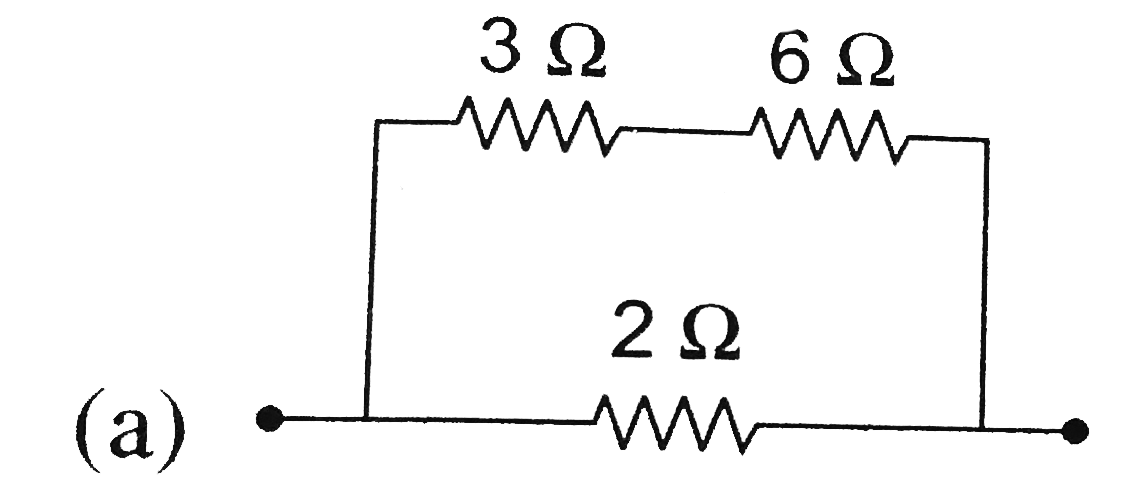 B
B C
C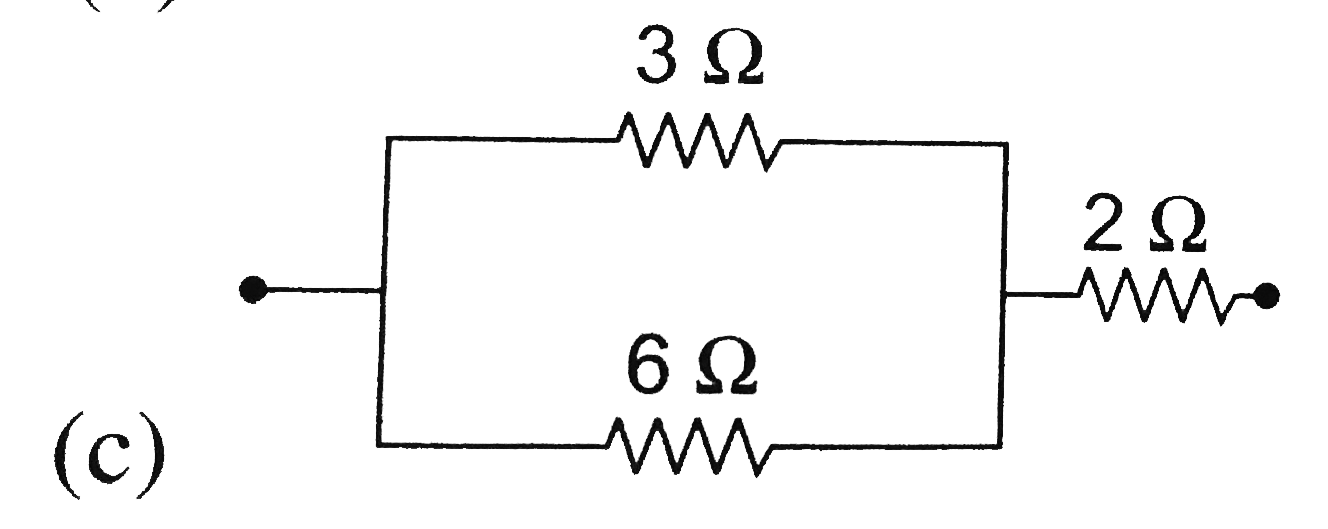 Dnone
Dnone
Given n resistors each of resistane R, how will you combine them to get the (i) maximum, (ii) minimum effective resistance ? What is the ratio of the maximum to minimum resistance ?
View Solution(a) Given n resistors each of resistance R. How will you combine them to get the (i) maximum (ii) minimum effective resistance ? What is the ratio of the maximum to minimum resistance ?
(b) Given the resistances of 1Ω,2Ω,3Ω, how will you combine them to get an equivalent resistance of (i) (11/3)Ω (ii) (11/5)Ω (iii) 6Ω (iv) (6/11)Ω ?
(c) Determine the equivalent resistance of networks shown in Figure.
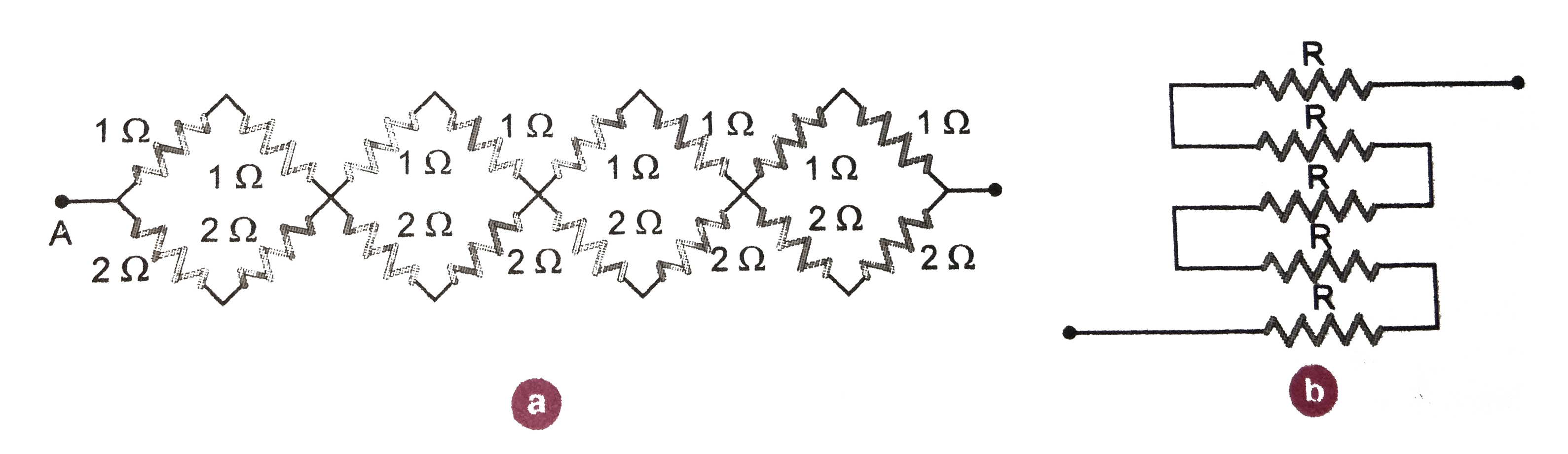
View Solution(a) Given n resistors each of resistance R. How will you combine them to get the (i) maximum (ii) minimum effective resistance ? What is the ratio of the maximum to minimum resistance ?
(b) Given the resistances of 1Ω,2Ω,3Ω, how will you combine them to get an equivalent resistance of (i) (11/3)Ω (ii) (11/5)Ω (iii) 6Ω (iv) (6/11)Ω ?
(c) Determine the equivalent resistance of networks shown in Figure.
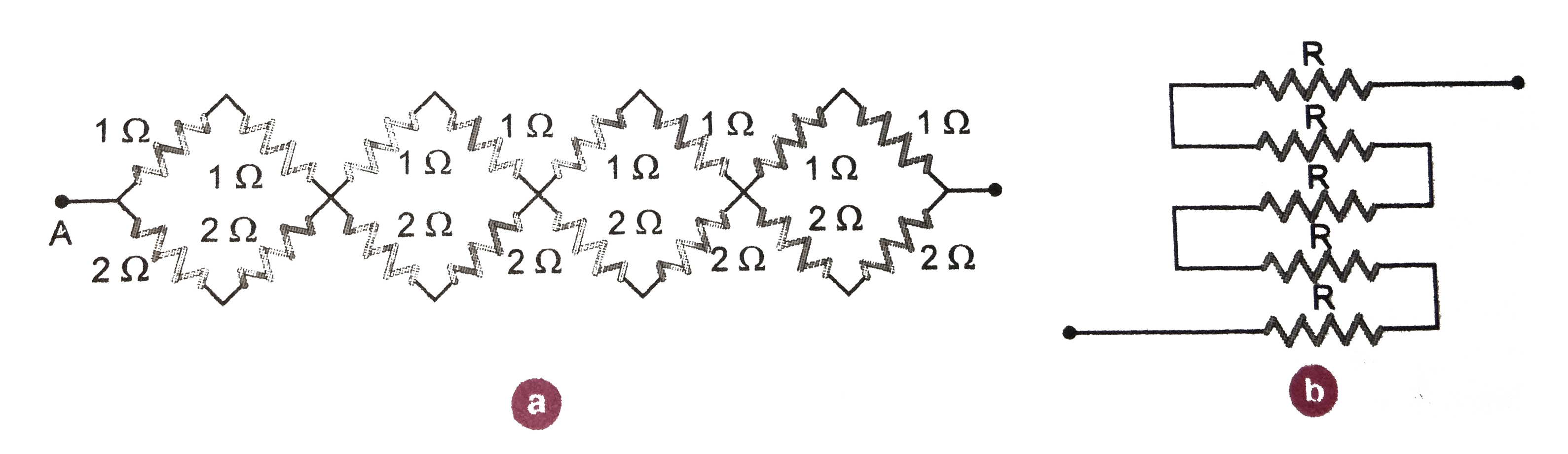
View SolutionGiven the resistances of 1Ω,2Ωand3Ω. How will you combine them to get an equivalent resistance of
(i) 113Ω ?
(ii) 115Ω ?
View SolutionGiven the resistances of 1Ω,2Ω,3Ω how will we combine them to get an equivalent resistance of (i) (113)Ω,(ii)(115)Ω,(iii)6Ω,(iv)(611)Ω ?
View SolutionGiven the resistance of 1Ω,2Ω,3Ω, how will you combine them to get an e3quivalent resistance of :
113Ω (ii)115Ω (iii)6Ω 611Ω ?
View SolutionGiven three resistors of resistances 1Ω,2Ωand3Ω. How will you combine them to get an equivalent resistance of 115Ω ?
View Solution
