In the following circuit a switch is initially connected to point A for a long time and them it is shifted to connect it to point B.

What will be the instantaneous current in the branch of the capacitor immediately after the switch is connected to point B?
The state of the circuit when switch is connected to point A and is kept closed for a long time is as shown in the following diagram.

After a long time a steady state is attained and the capacitor is fully charged. No current will be flowing through the branch of the capacitor and potential difference across 20Ω resistance will be applied across the capacitor. Current flowing in the loop is i=30/(10+20)=1A
Potential difference across 20Ω resistance
V=iR=1×20=20V
Hence, we know that the capacitor is charged to a potential difference of 20V.
Immediately after the switch is closed, we may assume the capacitor as a battery of 20V potential difference just for that moment only to calculate the current in 20Ω resistor. So equivalent circuit immediately after switch is connected to point B is as follows:

Applying Kirchhoff.s law for the loop CDHGC: 20−i1×20=0⇒i1=1A
Applying Kirchhoff.s law for the loop CDHEBFGC : 20+(i−i1)×10−10=0⇒i−i1=−1⇒i=0
So, no current flows in the branch of capacitor (shown as a battery of 20V emf) immediately after the switch is connected to point B.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - REVISION EXERCISES (VERY SHORT ANSWER QUESTIONS)
46 Videos
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - REVISION EXERCISES (ADDITIONAL QUESTIONS)
11 Videos
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - NCERT SOLVED (NCERT Exemplar Problems Subjective Questions)(Short Answers Type Questions)
6 Videos
- ATOMS BOOK - MODERN PUBLICATIONCHAPTER - ATOMS EXERCISE - Chapter Practice Test
16 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - CHAPTER PRACTICE TEST
15 Videos
Similar Questions
In the circuit shown, initially the switch is in position 1 for a long time. Then the switch is shifted to position 2 for a long time. Find the total heat produced in R2

View SolutionThe switch in figure Iis connected to position a for a long time interval. At t=0, the switch is thrown to position b. After this time , what are

View Solution
Knowledge Check
The switch in figure Iis connected to position a for a long time interval. At t=0, the switch is thrown to position b. After this time , what are
 Athe frequency of oscillation of the LC circuit is 200HzBthe maximum charge that appears on the capacitor is 12μC.Cthe maximum current in the indictor is 38mA (approx.)Dthe total energy the circuit possesses at t=3.00 s is 72μJ
Athe frequency of oscillation of the LC circuit is 200HzBthe maximum charge that appears on the capacitor is 12μC.Cthe maximum current in the indictor is 38mA (approx.)Dthe total energy the circuit possesses at t=3.00 s is 72μJ

What will be the resultant capacitance of the capacitors connected as shown in the figure between the points A and B?
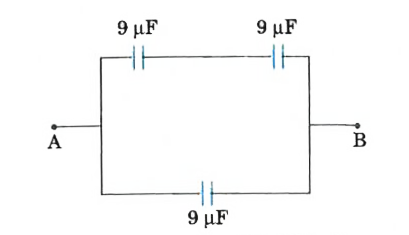 A11.5μFB12.5μFC13.5μFD14.5μF
A11.5μFB12.5μFC13.5μFD14.5μFWhat will be the resultant capacitance of the capacitors connected as shown in the figure between the points A and B ?
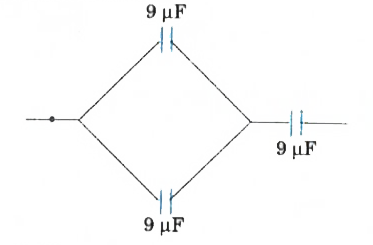 A6μFB2μFC27μFD4μF
A6μFB2μFC27μFD4μF
Initially the switch is in positions 1 for as long time then shifted to position 2 at t=0 as shown in figure. Just after closing the switch, the magnitude of current through the capacitor is

View SolutionSwitch is in position A for long time. At time t = 0 it is shifted to position B. Find the maximum charge that will accumulate on capacitor
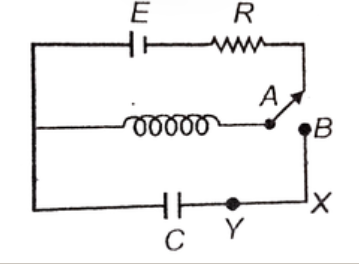
View SolutionSwitch is in position A for long time. At time t = 0 it is shifted to position B. Find the maximum charge that will accumulate on capacitor

View SolutionConsider the circuit shown in the figure. The switch has been in position 1 for a long time. Answer following questions:
(a) find current through 2R.
(b) find potential difference across the capacitor.
(c) At t=0 the switch is moved to position 2. What current flows through the capacitor immediately after the switch is placed to position 2?
(d) Draw a graph of current Vs time for the current through the capacitor after the switch is moved to position 2. Indicate the time on the graph when the current becomes 37% of its value immediately after the switch is put to position 2.
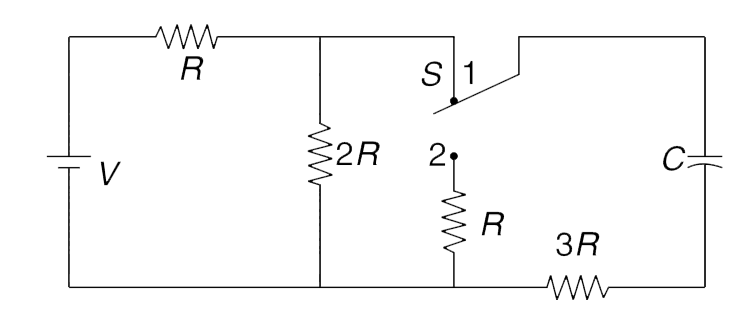
View SolutionInitially the switch is in positions 1 for as long time then shifted to position 2 at t=0 as shown in figure. Just after closing the switch, the magnitude of current through the capacitor is

View Solution
