A ring is made of a wire having a resistance R0=12Ω. Find the point A and B, as shown in the figure, at which a current carrying conductor should be connected so that the resistance R of the sub circuit between these points is equal to 83Ω.

l1l2=12
l1l2=58l
l1l2=13
l1l2=38
The correct Answer is:A
Resistance is proportional to the length for a given cross section of wire of a given material. Hence, the 12Ω resistance is divided proportional to length of the two parts. Let R1 be the resistance of length l1andR2 be the resistance of length l2, then we can write as follows:
R1=l1l1+l2×12=12l1l1+l2 ..(i)
Similarly we can write
R2=l2l1+l2×12=12l2l1+l2 ...(ii)
These two resistors connected in parallel given equivalent resistance 8/3Ω
1R1+1R2=38
⇒l1+l212l1+l1+l212l2=38
⇒l1+l2l1+l1+l2l2=92
⇒(1+l2l1)+(l1l2+1)=92
Let l1/l2 in the above equation be x. Then: ⇒1x+x=92−2
⇒1+x2x=52⇒2+2x2=5x
⇒2x2−5x+2=0
⇒x=5±√25−164=5±34
⇒x=2,12
Basically both answers imply that one part must be double to that of other part. Therefore, option (a) is correct.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - Objective Type Questions (MULTIPLE CHOICE QUESTIONS) (B. MULTIPLE CHOICE QUESTION JEE (MAIN) & OTHER STATE BOARDS FOR ENGINEERING ENTRANCE)
45 Videos
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - Objective Type Questions (MULTIPLE CHOICE QUESTIONS) (B. MULTIPLE CHOICE QUESTION JEE (ADVANCED) FOR IIT ENTRANCE)
9 Videos
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - Objective Type Questions (MULTIPLE CHOICE QUESTIONS) (A. MULTIPLE CHOICE QUESTIONS WITH ONLY ONE CORRECT ANSWER)
36 Videos
- ATOMS BOOK - MODERN PUBLICATIONCHAPTER - ATOMS EXERCISE - Chapter Practice Test
16 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - CHAPTER PRACTICE TEST
15 Videos
Similar Questions
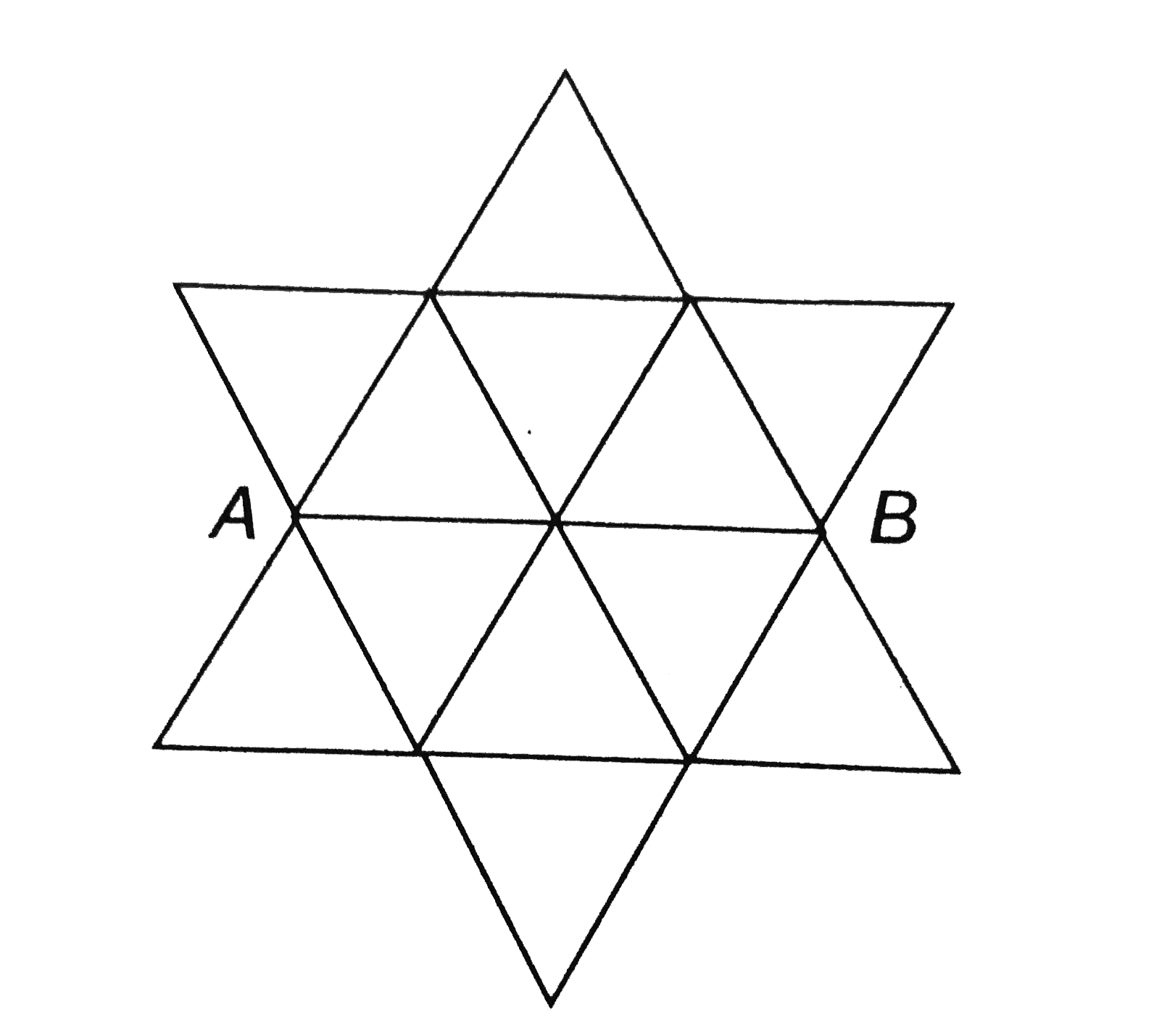
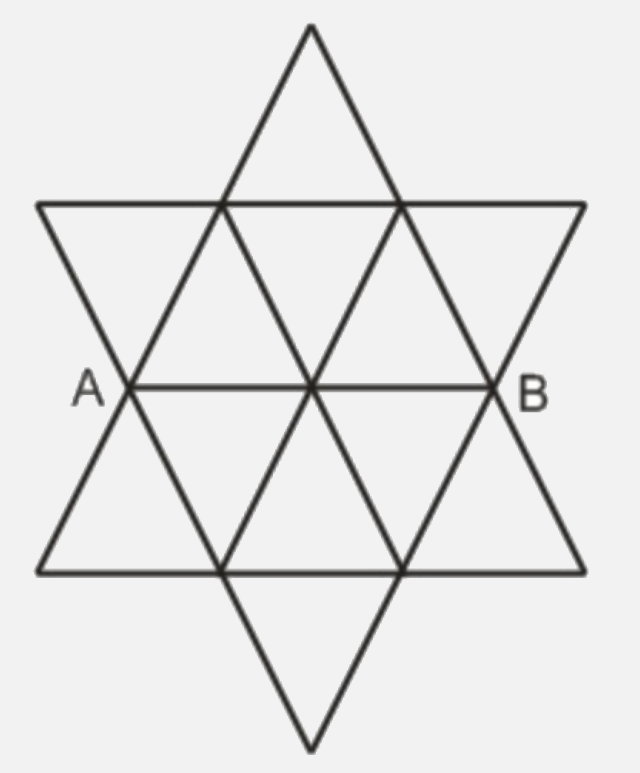
If the resistance of each branch of the circuit shown below is 1Ω , then the equivalent resistance of the circuit between the points A and B is
View SolutionIf the resistance of each branch of the circuit shown below is 1Ω , then the equivalent resistance of the circuit between the points A and B is
View Solution
Knowledge Check
In the network shown in the figure, each of the resistance is equal to 2Ω. The resistance between the points A and B is
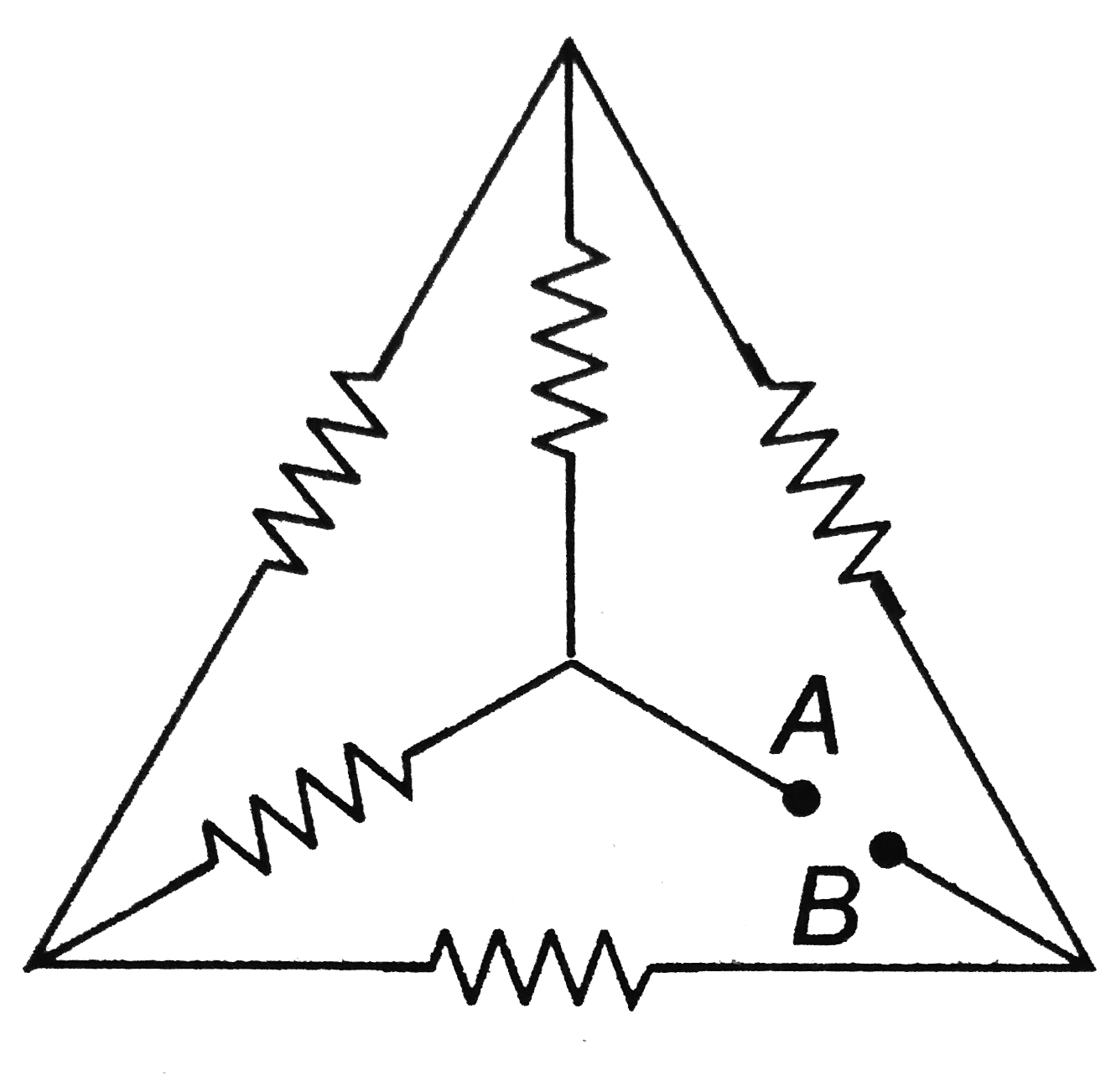 A1ΩB4ΩC3ΩD2Ω
A1ΩB4ΩC3ΩD2ΩA battery of internal resistance 4Ω is connected to the network of resistance as shown . In order that the maximum power can be delivered to the network, the value of R in Ω should be
 . A49B2C83D18
. A49B2C83D18Find the equivalent resistance of the circuit between points A and B shown in figure is (: each brach if of resistance 01Ω)
 A2225ΩB1225ΩC2235ΩD1235Ω
A2225ΩB1225ΩC2235ΩD1235Ω
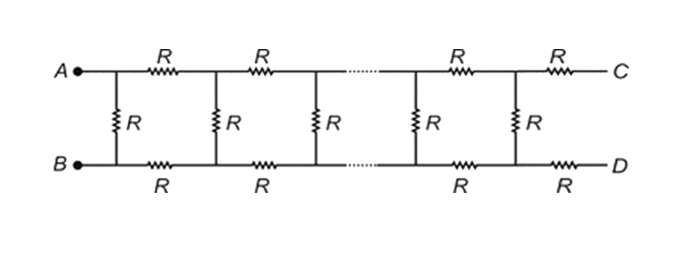
In the circuit shown, the resistance of each of resistor is R=100Ω. Find the nearest integer, which is to be connected points C and D so that the resistance of entire ciruit between A and B does not depend on the number of elementary cells.
View SolutionCalculate the value of resistance R in the circuit shown in the figure so that the current in the circuits is 0.2A. What would be the potential difference between the points B and E ?
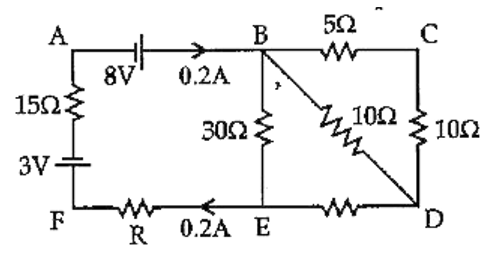
View SolutionTwelve resistors each of resistance 1Ω are connected in the circuit shown in figure. Net resistance between point A and H would be

View SolutionTwelve resistors each of resistance 1Ω are connected in the circuit shown in figure. Net resistance between point A and H would be

View SolutionFive 1Ω resistance are connected as shown in the figure. The resistance in the conneting wires is negligilbe. The equivalent resistance between A and B is
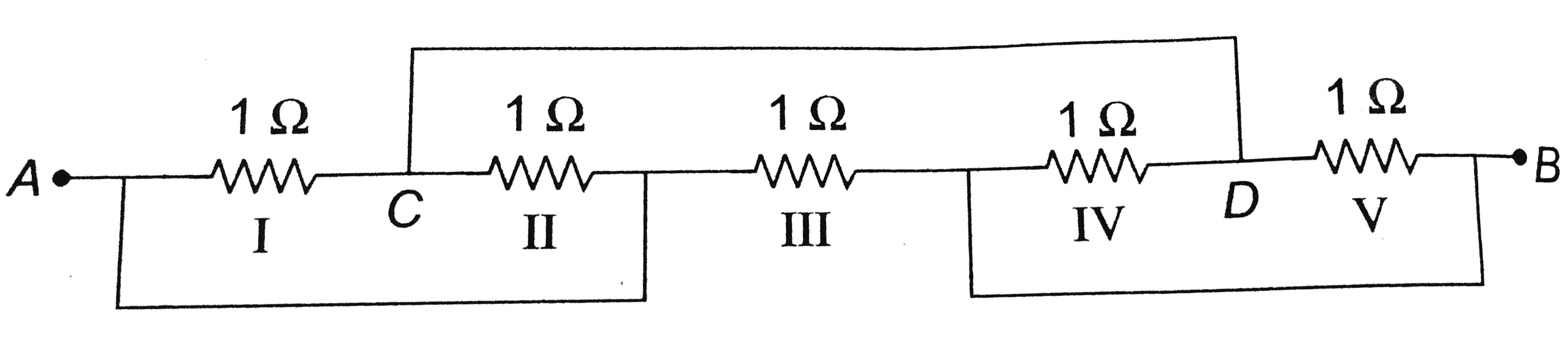
View Solution
