Two batteries with emf 12V and 13V are connected in parallel across a load resistor of 10Ω. The internal resistances of the two batteries are 1Ωand2Ω respectively. The voltage across the load lies between
11.4V and 11.5V
11.7 V and 11.8V
11.6V and 11.7V
11.5 V and 11.6V
The correct Answer is:D
To solve the problem of finding the voltage across the load resistor when two batteries are connected in parallel, we will follow these steps:
Step 1: Identify the given values
- EMF of Battery 1 (E1) = 12 V
- Internal resistance of Battery 1 (R1) = 1 Ω
- EMF of Battery 2 (E2) = 13 V
- Internal resistance of Battery 2 (R2) = 2 Ω
- Load resistance (R_load) = 10 Ω
Step 2: Calculate the equivalent EMF (E_eq)
The formula for the equivalent EMF when batteries are connected in parallel is given by:
Eeq=E1R2+E2R1R1+R2
Substituting the values:
Eeq=12×2+13×11+2=24+133=373 V≈12.33 V
Step 3: Calculate the equivalent internal resistance (R_eq)
The equivalent internal resistance for two resistors in parallel is given by:
Req=R1R2R1+R2
Substituting the values:
Req=1×21+2=23 Ω≈0.67 Ω
Step 4: Calculate the total resistance in the circuit
The total resistance in the circuit (R_total) is the sum of the equivalent internal resistance and the load resistance:
Rtotal=Req+Rload=23+10=23+303=323 Ω≈10.67 Ω
Step 5: Calculate the total current (I)
Using Ohm’s law, the total current flowing through the circuit can be calculated as:
I=EeqRtotal=373323=3732 A≈1.15625 A
Step 6: Calculate the voltage across the load resistor (V_load)
The voltage across the load resistor can be calculated using Ohm’s law:
Vload=I×Rload=3732×10=37032 V≈11.56 V
Conclusion
The voltage across the load lies between 11.5 V and 11.6 V.
- EMF of Battery 1 (E1) = 12 V
- Internal resistance of Battery 1 (R1) = 1 Ω
- EMF of Battery 2 (E2) = 13 V
- Internal resistance of Battery 2 (R2) = 2 Ω
- Load resistance (R_load) = 10 Ω
The formula for the equivalent EMF when batteries are connected in parallel is given by:
Eeq=E1R2+E2R1R1+R2
Substituting the values:
Eeq=12×2+13×11+2=24+133=373 V≈12.33 V
The equivalent internal resistance for two resistors in parallel is given by:
Req=R1R2R1+R2
Substituting the values:
Req=1×21+2=23 Ω≈0.67 Ω
The total resistance in the circuit (R_total) is the sum of the equivalent internal resistance and the load resistance:
Rtotal=Req+Rload=23+10=23+303=323 Ω≈10.67 Ω
Using Ohm’s law, the total current flowing through the circuit can be calculated as:
I=EeqRtotal=373323=3732 A≈1.15625 A
The voltage across the load resistor can be calculated using Ohm’s law:
Vload=I×Rload=3732×10=37032 V≈11.56 V
The voltage across the load lies between 11.5 V and 11.6 V.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - Objective Type Questions (MULTIPLE CHOICE QUESTIONS) (B. MULTIPLE CHOICE QUESTION JEE (ADVANCED) FOR IIT ENTRANCE)
9 Videos
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - Objective Type Questions (MULTIPLE CHOICE QUESTIONS) (C. MULTIPLE CHOICE QUESTIONS WITH MORE THAN ONE CORRECT ANSWER)
18 Videos
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - Objective Type Questions (MULTIPLE CHOICE QUESTIONS) (B. MULTIPLE CHOICE QUESTION FOR COMPETITIVE EXAMINATIONS)
20 Videos
- ATOMS BOOK - MODERN PUBLICATIONCHAPTER - ATOMS EXERCISE - Chapter Practice Test
16 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - CHAPTER PRACTICE TEST
15 Videos
Similar Questions
Two batteries A and B whose emf is 2V are connected in series with external resistance R=1Ω. Internal resistance of battery A is 1.9Ω and that of B is 0.9Ω.
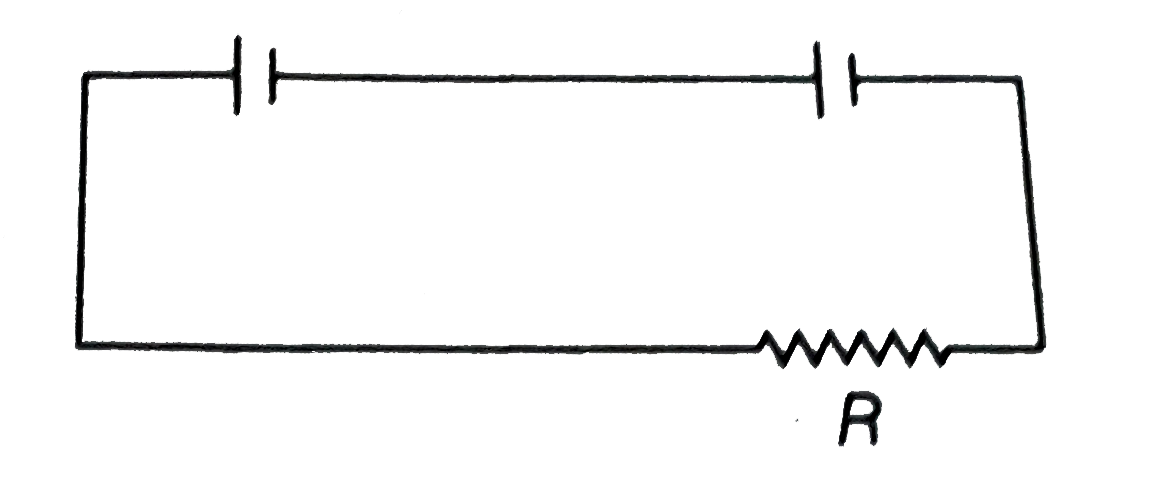
View SolutionThe series combination of two batteries, both of the same emf 10 V, but different internal resistance of 10Ω and 5Ω is connected to the parallel combination of two resistors 30Ω and RΩ . The voltage difference across the battery of internal resistance 10Ω is zero, the value of R (in Ω ) is : _________.
View Solution
Knowledge Check
Two batteries with emf 12 V and 13V are connected in parallel across a load resistor of 10Ω . The internal resistances of the two batteries are 1Ωand2Ω respectively . The voltage across the load lies between
A11.7 V and 11.8 VB11.6 V and 11.7 VC11.5 V and 11.6 VD11.4 V and 11.5 V4 cells each of emf 2 V and internal resistance of 1Ω are connected in parallel to a load resistor of 2Ω. Then the current through the load resistor is
A2AB1.5AC1AD0.888AThe cell has an emf of 2V and the internal resistance of this cell is 0.1Ω, it is connected to resistance of 3.9Ω, the voltage across the cell will be
A1.95VB1.90VC0.50VD2.00V
The series combination of two batteries both of the same emf 10 V, but different internal resistance of 20Ω and 5Ω is connected to the parallel combination of two resistors 30Ω and RΩ . The voltage difference across the battery of internal resistance 20Ω is zero, the value of R(in Ω) is __________.
View SolutionThree batteries having emfs and internal resistances as shown in figure are connected across a resistor of 2Ω. The reading of ammeter is
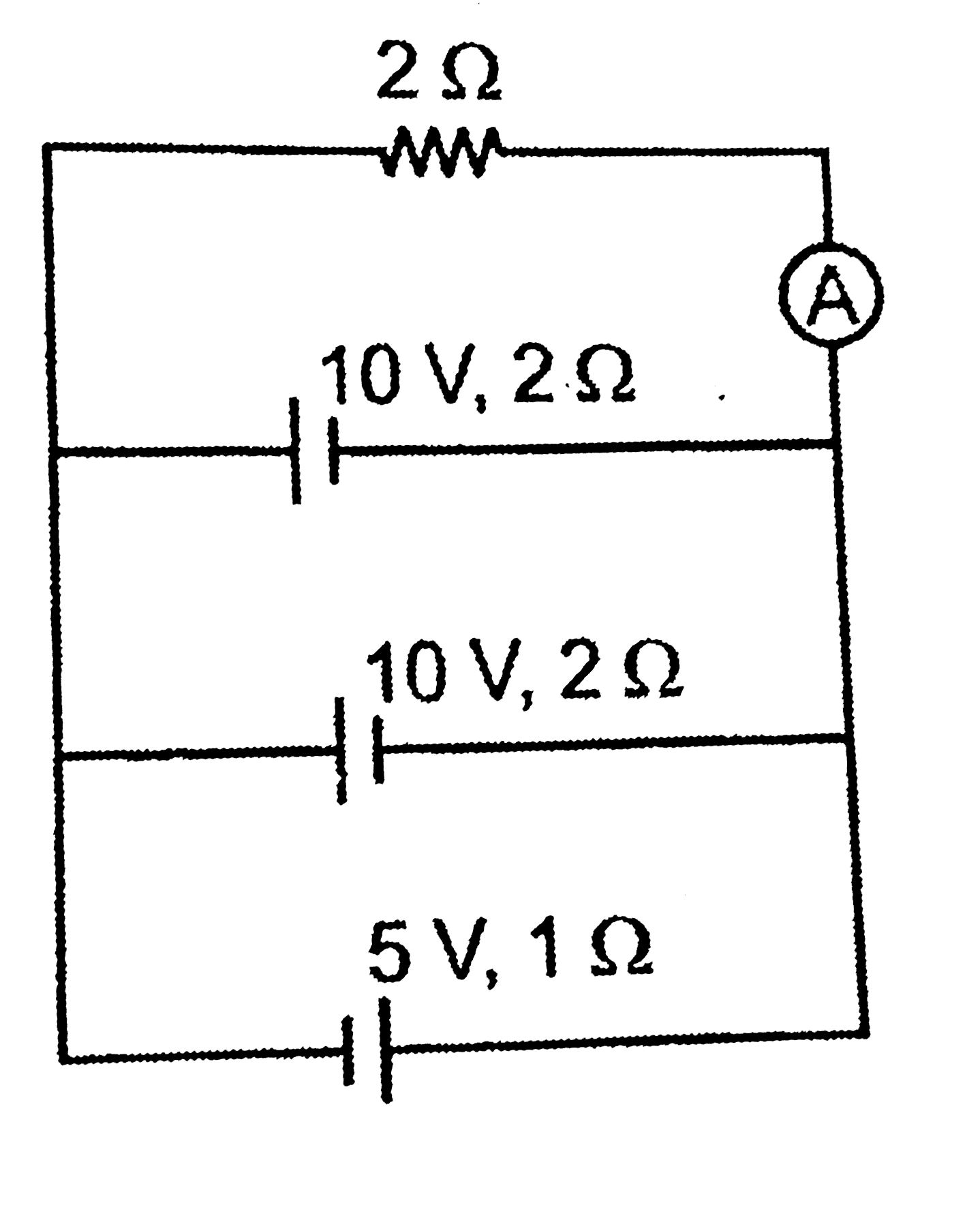
View SolutionThe cell has an emf of 2 V and the internal resistance of this cell is 0.1Ω, it is connected to resistance of 3.9Ω, the voltage across the cell will be
View SolutionThe cell has an emf of 2V and the internal resistance of this cell is 0.1Ω, it is connected to resistance of 3.9Ω, the voltage across the cell will be
View SolutionA cell of emf 2.0 V and internal resistance 0.1 Ω is connected with a resistance of 3.9Ω. The voltage across the cell terminals will be
View Solution